Трапецовидна формула (площ и периметър) с примерни въпроси + дискусия

Сигурно сте извършили броенето оттогавапърво, когато бях малко дете досега. Тъй като броенето винаги се случва в живота на всеки, не е чудно, че математиката се е превърнала в предмет, който се преподава още от детската градина.

Разбира се, нивото на трудност на уроците по математика на всяко ниво на образование е различно. По уникален начин математиката винаги е предмет, който ще определи интелекта на човек.

Колкото по-добри сте оценките си по математикавсе по-често ще се смята за умен човек. Може би това се основава и на факта, ако има някои математически проблеми, които са много трудни за правене. Така че математиците често се разглеждат като гении.

Трапецовидна формула

Определението за трапецовид е формаплосък, който има две измерения и е подреден от 4 страни, които са успоредни, но не с еднаква дължина. Трапецоидът също се формира от 4 ребра, където 2 ребра също са успоредни един на друг, но имат различна дължина. Трапецовидната сграда има няколко характеристики, които я отличават от другите сгради, включително:

1. Има 1 игрална симетрия
2. Имайте тъп ъгъл най-малко 1 ъгъл
3. Има 4 върха
4. Има 2 страни успоредни на различни дължини
5. Трапецът е плоска форма с 4 страни или четириъгълник

Говорейки за трапец, разбира се, че иматезнаете дали за изчисляване на площта и обиколката на трапец е необходима формула. Формулите на площта и обиколката на трапеца са следните:

А. Широка формула на трапецовидната

Общата формула за трапеца като цяло е:

Площ = ½ × брой успоредни ребра × височина

Въпреки това, формулата по-горе може да бъде променена и коригиранас трапецовидна форма. Има 3 форми на трапец, а именно десен трапец, равнобедрен трапец и просто всеки трапецоид. Обяснение на формулата за изчисляване на площта на тези три типа трапецовид е:

1. Широката формула на лакътя трапец

Както подсказва името, правоъгълният трапец етрапецовидна форма с два прави ъгъла или страни, които са успоредни и перпендикулярни една на друга във височината на трапеца. Или бихте могли да кажете, че един от ъглите в трапеца на десния лакът има големи 90 °.

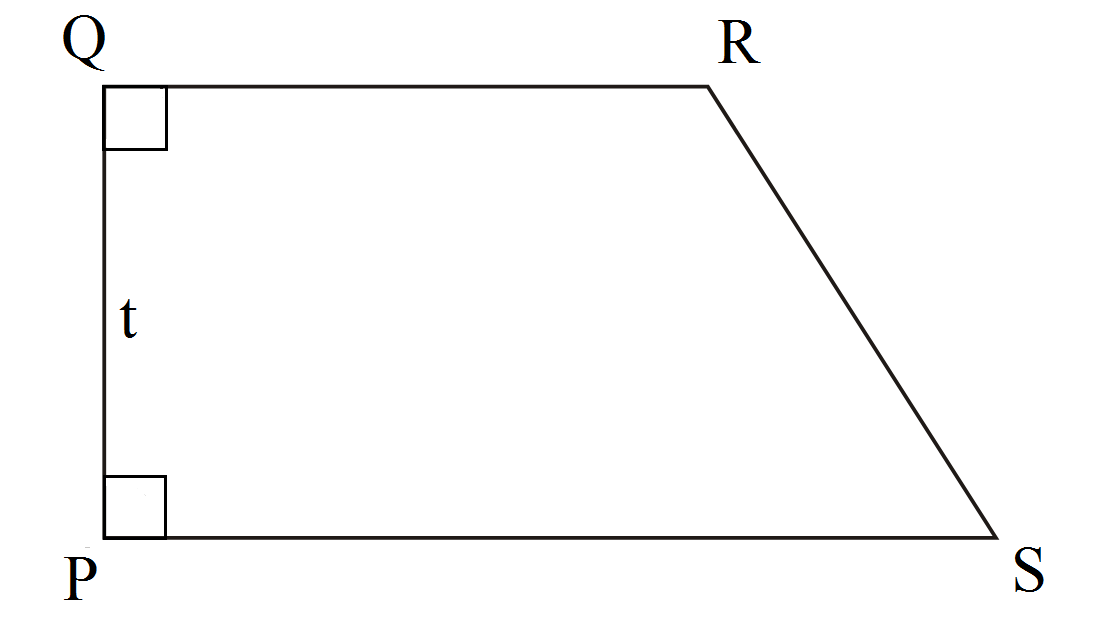
Широка формула за трапецовиден прав ъгъл PQRS: (PQ + RS) × t / 2

2. Изоситна трапецовидна широка формула

В допълнение към правоъгълния трапец, вид събужданедругият трапецовид е равнобедрен трапец. Когато равнобедрен трапец е трапец, който има една страна на сгъваема симетрия и ребра със същата дължина и подравняване. За повече подробности можете да видите от снимката по-горе.

KLMN равнобедрена трапецовидна широка формула: (LM + KN) × t / 2

3. Всяка широка трапецовидна формула

От снимката по-горе, разбира се, че вече знаетезащо този трапецоид се нарича просто всеки трапец. Това е така, защото в който и да е трапецовид от ABCD по-горе, изобщо няма симетрия на сгъване. Дори размерът на ребрата не е с еднаква дължина и е неправилен.

Всяка формула за трапец на ABCD: (BC + AD) × t / 2

Б. Трапецовидната формула

За да разберете обиколката на трапец тогаваПърво трябва да използвате формулата около трапеца. Тъй като формулата за площта на трапеца може да се използва само за определяне на площта, а формулата за обиколка на трапеца се използва за определяне на обиколката на всеки тип трапеция.

Трапецовидната формула: AB + BC + CD + DA

От горната формула може да се заключи, ако обиколката на трапеца е получена от сбора от всички страни на трапецовидна структура.

1. Формулата за трапецовидния лакът

В десния трапец има и периферна формула, която е:

Около трапецовидния лакът PQRS = PQ + QR + RS + SP

2. Формулата за пътуване около равнобедрени

Докато формулата около равнобедрения трапец е:

Около Trapezoid Isosceles KLMN = KL + LM + MN + NK

3. Всичко около формулата на трапеца

По принцип формулата около трапец с различни видове е една и съща. Окръжната формула за произволен трапец е:

Случайно всичко около ABCD = AB + BC + CD + DA

От третата формула различна пътуваща формулапри изграждането на трапеца по-горе може да се заключи, независимо от формата на трапеца, формулата на обиколката остава една. Но в трапецовида има не само широка и кръгла формула, но има формула, която използва питагоровата теорема, особено за трапецини с права ъгъл. Формулата е:

Формула с трапецовидна форма с висок ъгъл

Странична наклонена формула (в) десен трапец

Основна странична формула (а) десен трапец

Е, това беше пример за трапецовиден проблем, както и цялостна дискусия. Дано е полезно за вас.