Формула за изграждане на пространство и примери за въпроси и дискусии

Сигурно сте чували думата да се събуждате честопространство по време на изучаване на математика в училище. Видове различни видове сгради. Сградното пространство може да се интерпретира като обект или стая с триизмерна форма, която има както съдържание, така и обем и има граници (страни).

Е, пример за изграждане runag е кубчета, греди, триъгълни призми, правоъгълна пирамида, триъгълна пирамида, конуси, тръби и топки.

Всяка сграда има площ и топка. За да разберете по-добре формулата, използвана за намирането му, давай изслушах обяснение на формулата за изграждане на пространство и примери за проблема по-долу:

Формула за космическо изграждане

1. Кубът

Какво е кубче? Кубчето е a изграждане на пространство the the плоска страна, където всички ребра са с еднаква дължина както и всички страни с квадратна форма. Например зарове, рубик, картон и други.

Преди да обсъдим формулата на runag, първо знайте, каква е природата на куба? Е, тук е естеството на куба:

Пресейте свойствата на куба:

• Всички страни на куба са правоъгълни
• Има 8 върха
• Има 12 ребра със същата дължина
• Има 12 диагонални равнини (странични диагонали) с еднаква дължина
• Има 4 диагонала с еднаква дължина
• Има 6 странични броя
• Има 6 правоъгълни диагонални полета

Тъй като кубът е сградно пространство, разбира се има нещатрябва да изчислим, като обем или площ. Ето някои формули, които можете да използвате за решаване на проблеми в куб:

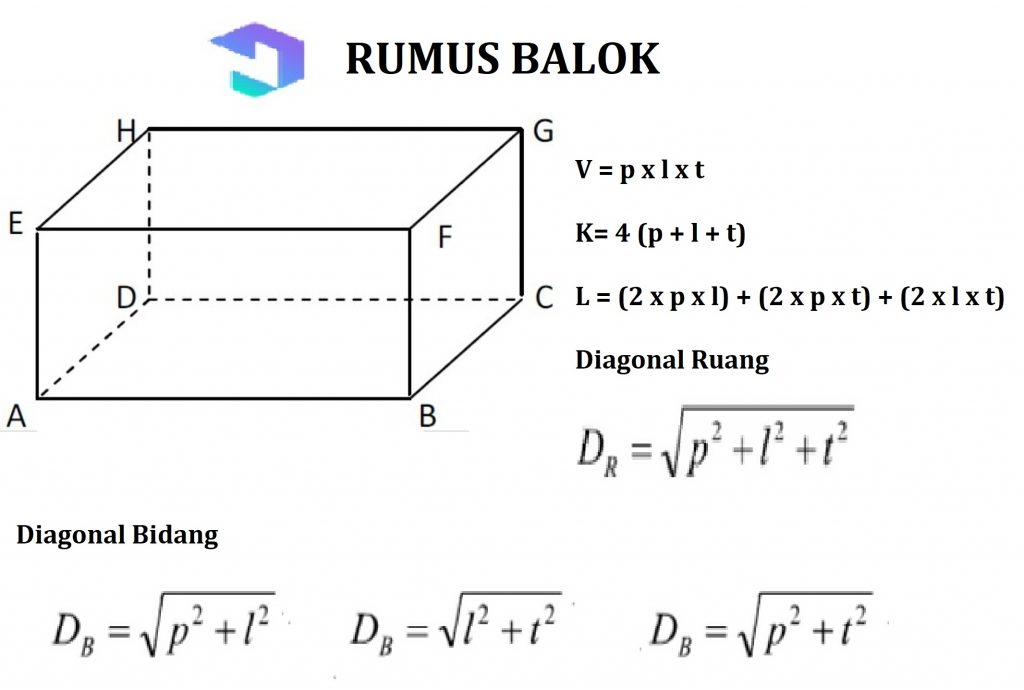
2. Греди

Изградете плоска странична стая втората е гредата, с 3 чифта страни с размер и форма както и изправени един срещу друг, Правоъгълна странична форма.

Свойствата на лъча:

• Като има страна с дълга форма persengi
• Има ребра успоредни на същия размер
• Да имат диагонали един към друг и една и съща дължина
• Има една и съща дължина диагонално пространство

3. Триъгълни призми

призма е изграждане на пространство който има поле на пиедестал и горно поле the the съответен и успоредна, Причината, поради която е конгруентна и равна, да защото другата страна на призмата е изправена, а формата е jajargenjang или правоъгълна. Конгруентът е конгруентен и равен.

Има няколко типа призми като петоъгълната призма, четириъгълната призма и триъгълната призма. Това, което го отличава, е броят на формите на основата и покрива, които има.

Свойствата на триъгълна призма:

• Той има 3 конгруентни покрива и основи.
• Всяка страна отстрани като стълба на стълба и правоъгълна
• Като цяло имат изправени ребра (някои не са изправени)
• Всяка диагонална равнина от една и съща страна има същия размер

Следните формули обикновено се използват за намиране на повърхност, обем на триъгълни призми:

4. Четириъгълни лимити

Четириъгълна пирамида е a изграждане на пространство който има основа с правоъгълна форма Обикновено пирамидата има странична равнина, която е изправена и триъгълна по форма, и опира в една точка, защото се пресича.

По-долу са формули, които могат да се използват в четириъгълна пирамида:

5. Триъгълни лимити

Триъгълни лимити е a изграждане на пространство който има триъгълна основа. Обикновено пирамидата има изправена странична равнинаи са триъгълни по форма и почиват на една точка, защото се пресичат. Това, което отличава името на пирамидата, е формата на основата, която покрива, като пирамидата на петоъгълника, четириъгълната пирамида и триъгълната пирамида.

По-долу са формули, които могат да се използват в пирамида:

6. Шишарки

Конус е стая с оформена основакръг и има странично равнинно одеяло и е оформено от кръг като клин. Често трябва да виждате шапки за рожден ден или шапки за шапки за фермерите. Е, тя е пример за форма на конус.

Характеристики на шишарки:

• Имайте 2 ребра
• Да има връх като среща на върха
• Има 2 броя странични равнини (страните на кръга се състоят от едно и като основа и едно одеало)

По-долу са формули, които могат да се използват за решаване на задачи в конусното пространство пространство:

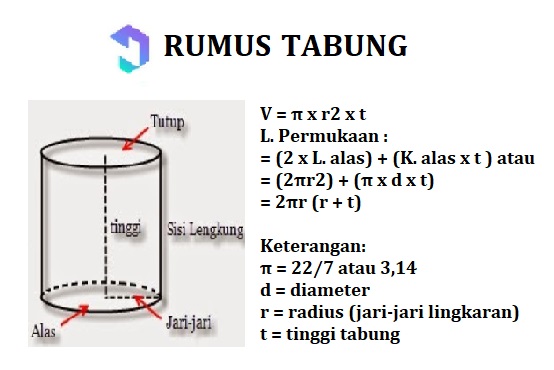
7. Тръба

Тръбата е a изграждане на пространство състоящ се от пиедестал и покрийте тази форма кръгът, както и да има извито одеяло, отстрани правоъгълник.

Свойства на тръбата:

• Имате мат и капак със същия размер
• Имайте 2 ребра
• Има 3 полета (2 кръга и 1 правоъгълник)
• Да няма връх

Обща формула за изчисляване на площта и обема на тръбите:

8. Топка

Много често виждаме топката в ежедневието, дори някои от вас наистина харесват игри с топка. Да, топката е тази, която събужда мястоимат площ и също обем. Това се отнася и до това защо топката може да се дриблира и контролира лесно, защото двете неща са отговорът.

Свойства на топката:

• Той няма върхове и ребра
• Имайте същото разстояние до центъра в точката на кривата.

Следва формула за намиране на обема и площта на сферата:

Примерни въпроси + Дискусията

1. Рубикът има дължина на страната 5 cm. Какъв е обемът на рубика?

Отговор:

V = s x s x s

= 5 x 5 x 5

= 125

Така обемът на рубика 125 см³

2. Блокът е с дължина 8 см, ширина 5 см и височина 4 см. Каква е обиколката на блока?

K = 4 (p x l x t)

= 4 (8 x 5 x 4)

= 640

Значи обиколката на гредата е 640 см

3. Разберете какъв е обемът на триъгълната призма, ако площта на основата е 16 см, а височината е 10 см!

Отговор:

V = L основа x t

= 16 х 10

= 160

Значи силата на звука 160 см²

4. Изчислете обема на правоъгълната пирамида, ако е дълга 6 см, ширина 4 см и височина 9 см

Отговор:

V = 1/3 (p x l x t)

= 1/3 (6 x 4 x 9)

= 71

Значи обемът на правоъгълната пирамида е 72 см²

5. Изчислете обема на триъгълната пирамида, ако площта на основата е 24 см, а височината е 5 см?

Отговор:

V = 1/3 (L основа x t)

= 1/3 (24 х 5)

= 40

Значи повърхността е 40 см²

6. Шапката за рожден ден има радиус 7 см, каква е основата на шапката?

Отговор:

L основа = πr²

= 7/22 x 7²

= 154

Толкова широка основна шапка за рожден ден 154 см

7. Радиусът на тръбата е 15 cm. Ако височината е 20 см, тогава обемът на тръбата е ...

Отговор:

V = πr²т

= 3,14 x 15² x 20

= 14,130

Значи обемът на тръбата е 14 130 см²

8. Велосипедното колело има радиус 14 cm. Определете повърхността на колелото за велосипеди!

Отговор:

L = 4πr²

= 4 x 22/7 x 14²

= 2464

Така че повърхността на колелата за велосипеди, чиито спици са 14 см 2464 см²

Това е дискусията за формулата за строително пространство (повърхност и обем на всяко сградно пространство) в комплект с примерни проблеми и дискусия. Надяваме се полезен и лесен за разбиране!