Vzorec pro objem krychlí a povrchovou plochu krychlí a příklady problémů

Dříve jsme diskutovali o vzorcíchobjem trubice, a pak ještě diskutovat o budování prostoru, tentokrát bude diskutovat vzorec pro nalezení objemu krychle. Kostka je budova s 12 ovocnými žebry stejné délky a skládá se ze 6 stran, které mají tvar čtverce

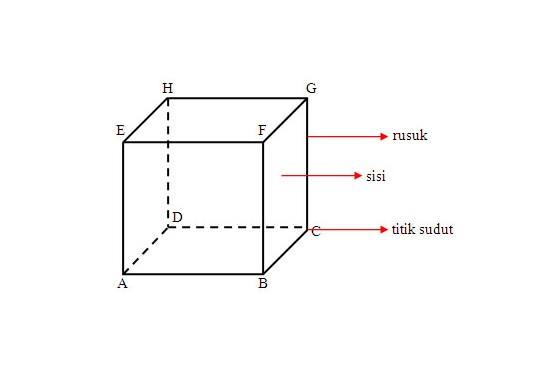
Kostka má obvykle části, a to: rovinnou stranu, žebro, diagonální rovinu, vrchol, diagonální stranu a diagonální prostor. Podobně i ostatní kostky, které mají objem hej. Pro více informací se podívejme na níže uvedené vysvětlení!

Vzorce objemu krychle

Před diskutováním objemu krychle nejprve diskutujeme prvky související s jejím objemem.

Pole / strana

Oblast / strana krychle je něco, co je krychlí ohraničeno. Ne, krychle má 6 stran, které mají stejnou délku ve tvaru čtverce.

Část boku krychle:

Horní strana (EFGH)
Spodní strana (ABCD)
Přední strana (ABFE)
Zadní strana (DCGH)
Pravá strana boku (ADHE)
Levá boční strana (BCGF)

Žebra

Pda krychle linky, které mají průsečíky mezi 2 poli / stranami se nazývají žebra. Na obrázku výše, včetně kostkových žeber, jsou AB, AE, BC, BF, CD, CG, DA, DH, EF, HE, FG, GH.

Vrchol

Průsečík mezi 2 nebo 3 žebry v krychli se nazývá bod sudurování. Na obrázku nahoře se krychle skládá z 8 úhlů, konkrétně A, B, C, D, E, F, G, H.

Diagonální boční / diagonální rovina

Pokud je v každém rohu uvedena dlouhá čárakrycí kostka se vytvoří jako rovný trojúhelník. Čára je diagonální strana nebo rovina. Na základě výše uvedeného obrázku krychle existuje 12 diagonálních stran / polí, a to AC, AF, AH, BD, BE, BG, CH, DE, DG, EG, FC a HG.

Diagonální prostor

Linka v jednom prostoru se stanespojení mezi dvěma body směřujícími k sobě se nazývá úhlopříčka prostoru. Na základě výše uvedeného obrázku krychle jsou 4 diagonální prostory, konkrétně linie AG, BH, DF a EC.

Diagonální rovina

Pole vytvořené ze 2 řádkůdiagonální strana / rovina a 2 rovnoběžná žebra zvaná diagonální rovina. Na základě výše uvedeného obrázku krychle existují 4 diagonální pole, jmenovitě ABGH, ACGE, DBFH, EFCG.

Ne, po rozpoznání krychle dále diskutujeme vzorec najít svazek jo. Zvažte vzorec níže:

Vzorec objemu krychle a povrchová plocha krychle

Příklad otázek a diskuse

Následující text vysvětluje některé otázky týkající se objemu hotové trubice pojď pozorně sledujte, abyste pochopili!

1. Kostka s 15 cm dlouhými žebry. Vypočítejte objem krychle!

Odpověď:

s = 15 cm

Objem zkumavky

V = s³
= 15 cm x 15 cm x 15 cm
= 3375 cm³

Takže objem krychle je 3375 cm³

2. Pokud je objem krychle 343 cm³. Jaká je boční délka kostky?

Odpověď:

V = 343 cm³

pak, V = s³
343 cm³ = s³
s = ∛ 343
s = 7 cm

Takže Kostka má délku Strana 7 cm.

3. Rubik má stranu 5 cm. Určete objem rubik?

Odpověď:

V = s³
= 5 cm x 5 cm x 5 cm
= 125 cm³

Takže objem rubik je 125 cm³

4. Pokud je délka vzpěry 20 cm. Jaký je objem trezoru?

Odpověď:

V = strana x strana x strana
V = 20 cm x 20 cm x 20 cm
V = 8000 cm³

Takže objem trezoru je 8000 cm³

5. Vana má 2,5 cm dlouhá žebra, kolik vody může vana naplnit?

Odpověď:

V = strana x strana x strana
V = 2,5 m x 2,5 m x 2,5 m
V = 15 625 m³

Takže je potřeba hodně vody, aby byla plná vana 15 625 m³

6. Objem krabičky ve tvaru krychle je 729 cm³. Vypočítat, jaká je celková délka žebra krabičky?

Odpověď:

V = s³
729 = s³
s³ = 729
s = ∛ 729
s = 9 cm

Počet žeber = 12
Celkový počet žeber = 9 x 12 = 108 cm

Takže celková délka žeber krabice 108 cm.

7 Andi nalila vodu do vany ve tvaru kostky se 14 cm dlouhým žebrem. Množství vody, kterou vylil Andi, však představovalo pouze polovinu pánve. Kolik vody Andi nalil?

Odpověď:

Objem vody v lázni = objem 1/2 krychle
Objem vody ve vaně = ½ x s³

= 1/2 x 14 cm x 14 cm x 14 cm

= 1/2 x 2 444 cm³

= 1 372 cm³

Takže množství vody, kterou nalil Andi, je 1372 cm³.

8. Délka žeber krychle je 12 cm. pak nakrájíme na kostky o malé velikosti, která jsou 3 cm dlouhá žebra. Zjistěte, kolik malých kostek je vyrobeno?

Odpověď:
Objem velké krychle = 12 cm x 12 cm x 12 cm = 1,728 cm³
Objem malé krychle = 3 cm x 3 cm x 3 cm = 27 cm³
Celkový počet malých kostek = 1,728: 27 = 64

Takže součet všech malých kostek po krájení je 64 kusů

9. Jaká je diagonální oblast krychle, pokud je délka žebra 24 cm? (dik: √2 = 1 414)

Odpověď:

Plocha diagonální plochy = 24 cm x 24 cm x √2

= 10 cm x 10 cm x 1 414

= 814,464 cm²

Takže plocha úhlopříčky je 814,464 cm²

10. Krabice ve tvaru krychle s 10 cm žebry, načež se nakrájí na malé krabičky o objemu 500 cm³Spočítejte si kolik malých kostek máte celkem!

Odpověď:

Objem velké krabičky (krychle) = 10 cm x 10 cm x 10 cm = 1 000 cm^{3 </ polévka

Objem malé krychle = 500 cm^{3 </ polévka}}

Počet malých kostek = objem velkých kostek: objem malých kostek
Počet malých kostek = 1 000: 500 = 2 kusy

Takže součet všech malých kostek po krájení je 2 kusy

Ne, z výše uvedených otázek a diskuseMůžete snadno pochopit, jak řešit problémy, pokud se týkají vzorce pro stavbu krychle. Pro jednoduchost musíte nejprve zapamatovat vzorec, poté pochopit účel problému a co je v problému známo.

Číst dál: