Trapesformet formel (område og omkreds) med eksempler på spørgsmål + diskussion

Du skal have udført tælleaktiviteten sidenførst da jeg var et lille barn indtil nu. Fordi tælling altid sker i alles liv, er det ikke underligt, at matematik er blevet et emne, der er blevet undervist allerede siden børnehaven.

Naturligvis er vanskelighedsniveauet i matematikundervisningen på hvert uddannelsesniveau forskelligt. Unikt er matematik altid et emne, der bestemmer ens intelligens.

Jo bedre dine matematikklasser er duvil i stigende grad blive betragtet som en smart person. Måske er dette også baseret på det faktum, at hvis der er nogle matematiske problemer, der er meget vanskelige at gøre. Så at matematikere ofte betragtes som genier.

Trapesformet formel

Definitionen af trapezoid er en formflad, der har to dimensioner og er arrangeret af 4 sider, der er parallelle, men ikke af samme længde. Trapezoid er også dannet af 4 ribber, hvor 2 ribber også er parallelle med hinanden, men har forskellige længder. Trapesformet bygning har flere egenskaber, der adskiller den fra andre bygninger, herunder:

Har 1 legesymmetri
Har en stump vinkel mindst 1 hjørne
Har 4 hjørner
Har 2 sider parallelt med forskellige længder
Trapezoid er en flad form med 4 sider firsidede

At tale om trapezoid, har du selvfølgeligvide, om der er brug for en formel for at beregne en trapezoidareal og omkreds. Formlerne for området og trapesformet omkreds er som følger:

A. Trapesformet bred formel

Den brede formel for trapezoid generelt er:

Areal = ½ × antal parallelle ribben × højde

Imidlertid kan formlen ovenfor ændres og justeresmed trapesformet form. Der er 3 former for trapezoid, nemlig højre trapezoid, isosceles trapezoid og bare enhver trapezoid. Forklaring af formlen til beregning af arealet af disse tre typer trapes er:

1. Den brede formel for albue trapes

Som navnet antyder er retvinklet trapezoiden trapezformet form med to rette vinkler eller sider, der er parallelle og vinkelret på hinanden i trapezoidens højde. Eller du kan sige, at et hjørne i trapezoidet på en højre albue har en stor 90 °.

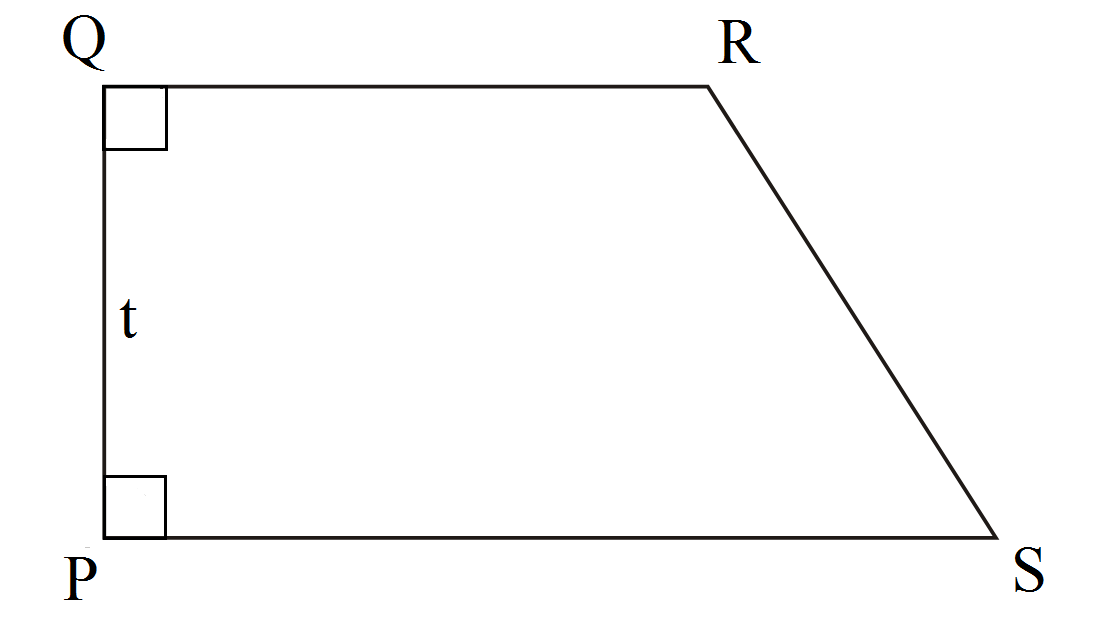
Bred formel til trapesformet højre vinkel PQRS: (PQ + RS) × t / 2

2. Isosceles trapesformet bred formel

Foruden den retvinklede trapezoid, slags vågne opden anden trapezoid er en isosceles trapezoid. Hvor isosceles trapezoid er en trapezoid, der har den ene side af foldesymmetri og ribber i samme længde og linie. For flere detaljer, kan du se fra billedet ovenfor.

KLMN isosceles trapesformet bred formel: (LM + KN) × t / 2

3. Enhver tilfældig trapesformet formel

Fra billedet ovenfor ved du selvfølgelig alleredehvorfor denne trapezoid bare kaldes enhver trapez. Dette skyldes, at der i enhver ABCD-trapezoid ovenfor ikke er nogen foldesymmetri overhovedet. Selv størrelsen på ribbenene er ikke af samme længde og er uregelmæssig.

Enhver ABCD-trapezformel: (BC + AD) × t / 2

B. Den trapesformede formel

At finde ud af omfanget af en trapezoid derefterDu skal først bruge formlen omkring trapezoidet. Fordi trapezoidarealformlen kun kan bruges til at bestemme området, og trapezoidomkretsformlen bruges til at bestemme omkredsen af hver type trapezoid.

Den trapesformede formel: AB + BC + CD + DA

Fra formlen ovenfor kan det konkluderes, hvis trapezoidets omkreds opnås fra summen af alle sider af en trapezformet struktur.

1. Formlerne for albue-trapes

I den rigtige trapezoid findes der også en perifere formel, som er:

Omkring trapesformet albue PQRS = PQ + QR + RS + SP

2. Formlen for at rejse rundt på ensben

Mens formlen omkring den isosceles trapezoid er:

Omkring trapesformet isosceles KLMN = KL + LM + MN + NK

3. Alt omkring trapesformen

Grundlæggende er formlen omkring en trapezoid med forskellige typer den samme. Omkretsformlen for enhver trapezoid er:

Tilfældig noget omkring ABCD = AB + BC + CD + DA

Fra den tredje formel forskellige rejseformelved opbygning af trapezoid ovenfor kan man afslutte, uanset hvilken form for trapezoid der er, forbliver omkretsformlen en. Men i trapezoidet findes der ikke kun en bred og cirkulær formel, men der er en formel, der bruger den pythagoreiske teorem, især til retvinklede trapeziner. Formlen er:

Højvinklet trapesformel

Formel side skrånende (c) højre trapez

Basissideformel (a) højre trapez

Eksempler på trapesformede problemer og diskussion

Efter at have lært om, hvad der er en trapezoid,egenskaberne, som trapezoidet besidder, og formlen indeholdt af trapezoidet. Så det er ufuldstændigt, hvis du ikke prøver at stille nogle spørgsmål om trapez. Nogle eksempler på trapesformede spørgsmål og løsninger nedenfor kan du lave materiale til læring.

1. En trapezoid har parallelle sider på 8 cm og 22 cm og en højde på 6 cm. Hvad er området med trapesformet?

svar:

Trapesformet område = antal parallelle x højder / 2 = (8 + 22) × 6/2 = 30 × 3 = 90 cm²

2. Hvis længden af de skrå sider af trapezoidet i problem 1 er 5, hvad er trapezoidets omkreds?

svar:

Trapesformets omkreds = længden af alle ribber = 8 + 22 + 5 + 5 = 40 cm.

3. Sluk for billedet herunder!

Beregn arealet og omkredsen af den ensartede trapezoid ovenfor!

svar:

Fordi KLMN trapezoid ovenfor er en isosceles trapezoid, er længden af LM = KN = 10 cm.

Så at omkredsen:
Omkrets = KL + LM + MN + KN
Omkrets = 12 + 10 + (18 + 6) + 10 = 56 cm

Trapesformet område:

For at beregne arealet skal vi førstskal kende trapezoidens højde (vinkellængde K og O). Bemærk på figuren, at vinklen NK O danner en højre trekant, så for at finde længden af vinklen K og O bruges følgende Pyytagoreiske formel:

KO = trapezoidhøjde = 8 cm.

Så at: