Φόρμουλα για τη δημιουργία χώρου και παραδείγματα ερωτήσεων και συζήτησης

Πρέπει να έχετε ακούσει τη λέξη ξυπνήστε συχνάδιάστημα ενώ μελετάτε τα μαθηματικά στο σχολείο. Τύποι διαφόρων τύπων κτιρίων. Ο χωροταξικός χώρος μπορεί να ερμηνευτεί ως ένα αντικείμενο ή ένα δωμάτιο με τρισδιάστατο σχήμα που έχει τόσο περιεχόμενο όσο και όγκο και έχει όρια (πλευρές).

Να, παράδειγμα κατασκευής runag κύβοι, δοκοί, τριγωνικά πρίσματα, ορθογώνια πυραμίδα, τριγωνική πυραμίδα, κώνοι, σωλήνες και σφαίρες.

Κάθε κτίριο έχει επιφάνεια και μπάλα. Για να κατανοήσουμε καλύτερα τον τύπο που χρησιμοποιήθηκε για να το βρείτε, yuk άκουσε μια εξήγηση για τον τύπο για την κατασκευή χώρου και παραδείγματα του παρακάτω προβλήματος:

Φόρμουλα διαστήματος

1. Ο κύβος

Τι είναι ένας κύβος; Ο κύβος είναι α να χτίσουν χώρο το επίπεδη πλευρά, όπου όλες οι πλευρές έχουν το ίδιο μήκος καθώς και όλες οι πλευρές ενός τετράγωνου σχήματος. Για παράδειγμα, τα ζάρια, το ρουμπίκ, το χαρτόνι και άλλα.

Πριν συζητήσουμε τον τύπο runag, πρώτα γνωρίζουμε ποια είναι η φύση του κύβου; Λοιπόν, εδώ είναι η φύση του κύβου:

Διαχωρισμός ιδιοτήτων του κύβου:

• Όλες οι πλευρές του κύβου είναι ορθογώνιες
• Έχει 8 κορυφές
• Έχει 12 πλευρές του ίδιου μήκους
• Έχει 12 διαγώνια επίπεδα (πλευρικές διαγώνιες) ίσου μήκους
• Έχει 4 διαγώνιες του ίδιου μήκους
• Έχει 6 πλευρικά κομμάτια
• Έχει 6 ορθογώνια διαγώνια πεδία

Επειδή ο κύβος είναι ένα κτίριο χώρου, φυσικά υπάρχουν πράγματαπρέπει να υπολογίσουμε, όπως ο όγκος ή η επιφάνεια. Ακολουθούν ορισμένοι τύποι που μπορείτε να χρησιμοποιήσετε για την επίλυση προβλημάτων σε έναν κύβο:

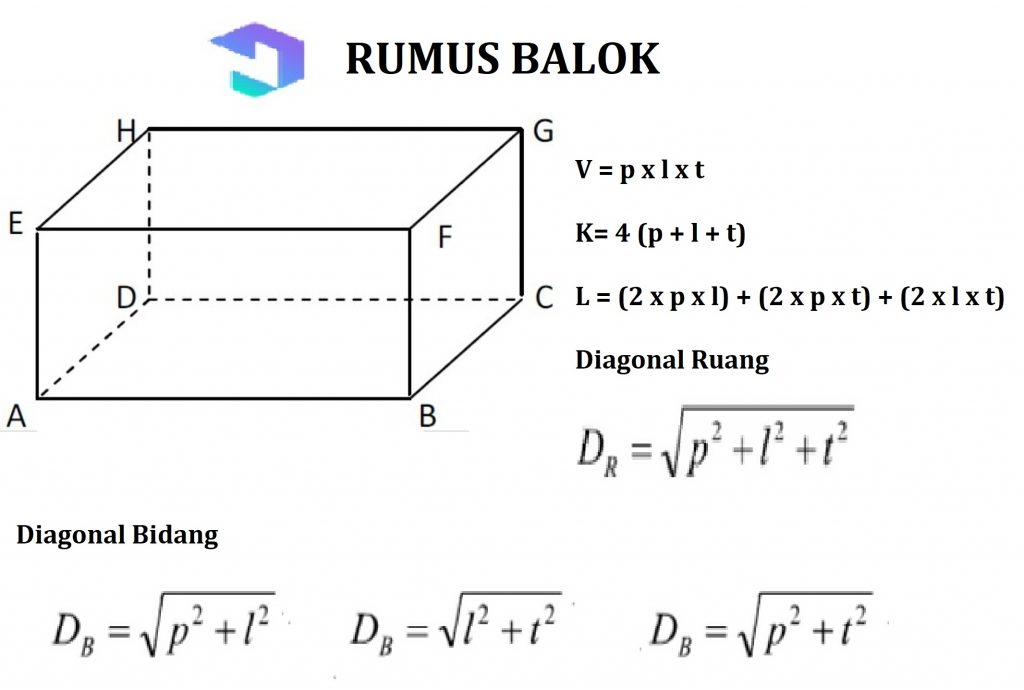
2. Δοκοί

Δημιουργήστε ένα επίπεδο πλευρικό δωμάτιο η δεύτερη είναι η ακτίνα, με 3 ζεύγη πλευρών με μέγεθος και σχήμα καθώς και αντιμετωπίζουν ο ένας τον άλλον. Ορθογωνική πλευρική μορφή.

Οι ιδιότητες της δοκού:

• Έχοντας μια πλευρά με μακρύ σχήμα persengi
• Έχοντας παράλληλες πλευρές στο ίδιο μέγεθος
• Να έχουν διαγώνια το ένα στο άλλο και το ίδιο μήκος
• Έχει το ίδιο διαγώνιο διάστημα μήκους

3. Τριγωνικά πρίσματα

Πρίσμα είναι να χτίσουν χώρο ποιος έχει πεζών και πάνω πεδίο το συνεπής και παράλληλα. Ο λόγος για τον οποίο είναι σύμφωνος και ισότιμος, ναι γιατί η άλλη πλευρά του πρίσματος είναι όρθια και το σχήμα είναι jajargenjang ή ορθογώνιο. Το Congruent είναι σύμφωνο και ίσο.

Υπάρχουν διάφοροι τύποι πρισμάτων όπως το πενταγωνικό πρίσμα, το τετράπλευρο πρίσμα και το τριγωνικό πρίσμα. Αυτό που διακρίνει είναι ο αριθμός των μορφών βάσης και οροφής που έχει.

Οι ιδιότητες ενός τριγωνικού πρίσματος:

• Διαθέτει 3 συμπαγείς στέγες και βάσεις.
• Κάθε πλευρά της πλευράς σαν σκάλα και ορθογώνια
• Γενικά έχουν όρθια πλευρά (μερικά δεν είναι όρθια)
• Κάθε διαγώνιο επίπεδο στην ίδια πλευρά, έχει το ίδιο μέγεθος

Οι ακόλουθοι τύποι χρησιμοποιούνται συνήθως για την εύρεση της επιφάνειας, του όγκου των τριγωνικών πρισμάτων:

4. Το τετράπλευρο Limas

Τετράπλευρη πυραμίδα είναι α να χτίσουν χώρο ποιος έχει ορθογώνια βάση. Συνήθως η πυραμίδα έχει πλευρικό επίπεδο που είναι όρθιο και τριγωνικό σε σχήμα και στηρίζεται σε ένα σημείο επειδή τέμνει.

Τα ακόλουθα είναι τύποι που μπορούν να χρησιμοποιηθούν σε τετράπλευρη πυραμίδα:

5. Τριγωνικά Λίμα

Τριγωνικά λιμά είναι α να χτίσουν χώρο ποιος έχει τριγωνική βάση. Συνήθως η πυραμίδα έχει ένα όρθιο πλευρικό επίπεδοκαι έχουν τριγωνικό σχήμα και στηρίζονται σε ένα σημείο επειδή τέμνονται. Αυτό που διακρίνει το όνομα της πυραμίδας είναι το σχήμα της βάσης που καλύπτει, όπως η πυραμίδα του πενταγώνου, η τετράπλευρη πυραμίδα και η τριγωνική πυραμίδα.

Ακολουθούν οι τύποι που μπορούν να χρησιμοποιηθούν σε μια πυραμίδα:

6. Κώνοι

Ένας κώνος είναι ένα δωμάτιο με διαμορφωμένη βάσηκύκλος και έχει πλευρική επίπεδη κουβέρτα και σχηματίζεται από κύκλο σαν σφήνα. Πρέπει συχνά να βλέπετε καπέλα γενεθλίων ή καπέλα για αγρότες. Να, είναι ένα παράδειγμα σχήματος κώνου.

Χαρακτηριστικά των κώνων:

• Έχετε 2 νευρώσεις
• Έχοντας μια κορυφή ως συνάντηση της κορυφής
• Έχει 2 πλευρικά επίπεδα (οι πλευρές του κύκλου αποτελούνται από ένα και ως βάση και ένα πεδίο κουβέρτας)

Ακολουθούν οι τύποι που μπορούν να χρησιμοποιηθούν για την επίλυση προβλημάτων στην κατασκευή κωνικού χώρου:

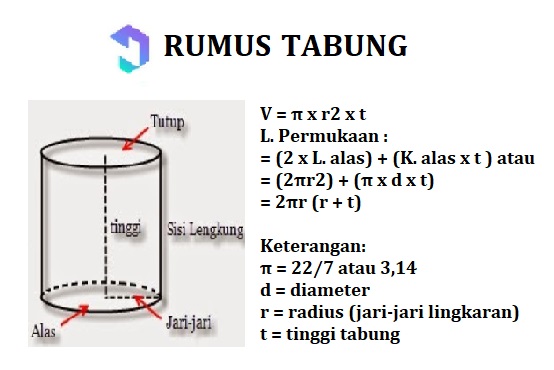
7. Σωλήνας

Ο σωλήνας είναι α να χτίσουν χώρο αποτελούμενη από βάση και κάλυμμα σε σχήμα τον κύκλο, καθώς και έχοντας καμπύλη κουβέρτα, από το πλάι ορθογώνιο.

Ιδιότητες του σωλήνα:

• Έχετε ένα χαλί και καπάκι του ίδιου μεγέθους
• Έχετε 2 νευρώσεις
• Έχει 3 πεδία (2 κύκλους και 1 ορθογώνιο)
• Δεν έχετε κορυφή

Γενικός τύπος για τον υπολογισμό της περιοχής και του όγκου των σωλήνων:

8. Μπάλα

Πολύ συχνά βλέπουμε την μπάλα στην καθημερινή ζωή, ακόμη και σε ορισμένους από εσάς αρέσει πολύ τα παιχνίδια με μπάλα. Ναι η μπάλα είναι μια που ξυπνά χώροέχουν εμβαδόν και επίσης όγκο. Αυτό σχετίζεται επίσης με το γιατί η μπάλα μπορεί να ντρίμπλα και να ελεγχθεί εύκολα επειδή τα δύο πράγματα είναι η απάντηση.

Ιδιότητες μπάλας:

• Δεν έχει κορυφές και νευρώσεις
• Έχετε την ίδια απόσταση από το κέντρο στο σημείο της καμπύλης.

Το παρακάτω είναι ένας τύπος για την εύρεση του όγκου και της επιφάνειας μιας σφαίρας:

Παράδειγμα Ερωτήσεις + Η συζήτηση

1. Ένα ρουμπίκ έχει πλευρικό μήκος 5 cm. Ποιος είναι ο όγκος του ρουμπίκ;

Απάντηση:

V = s x s x s

= 5 x 5 x 5

= 125

Έτσι, ο όγκος του ρουμπίκ 125 εκ³

2. Ένα μπλοκ έχει μήκος 8 cm, πλάτος 5 cm και ύψος 4 cm. Ποια είναι η περιφέρεια του μπλοκ;

Κ = 4 (p x l x t)

= 4 (8 x 5 x 4)

= 640

Έτσι, η περιφέρεια της δέσμης είναι 640 εκ

3. Μάθετε ποιος είναι ο όγκος του πρίσματος τριγώνου εάν η επιφάνεια βάσης είναι 16 cm και το ύψος είναι 10 cm!

Απάντηση:

V = L βάση x t

= 16 x 10

= 160

Έτσι ο όγκος 160 εκ²

4. Υπολογίστε τον όγκο της ορθογώνιας πυραμίδας εάν έχει μήκος 6 cm, πλάτος 4 cm και ύψος 9 cm

Απάντηση:

V = 1/3 (p x l x t)

= 1/3 (6 x 4 x 9)

= 71

Έτσι, ο ορθογώνιος όγκος της πυραμίδας είναι 72 εκ²

5. Υπολογίστε τον όγκο της τριγωνικής πυραμίδας εάν η επιφάνεια βάσης είναι 24 cm και το ύψος είναι 5 cm;

Απάντηση:

V = 1/3 (βάση L x x)

= 1/3 (24 x 5)

= 40

Έτσι, η επιφάνεια είναι 40 εκ²

6. Ένα καπέλο γενεθλίων έχει ακτίνα 7 cm, ποια είναι η βάση του καπέλου;

Απάντηση:

Βάση L = πr²

= 7/22 x 7²

= 154

Το καπέλο γενεθλίων ευρείας βάσης είναι 154 εκ

7. Η ακτίνα ενός σωλήνα είναι 15 cm. Εάν το ύψος είναι 20 cm, ο όγκος του σωλήνα είναι ...

Απάντηση:

V = πρ²t

= 3,14 x 15² x 20

= 14,130

Έτσι ο όγκος του σωλήνα είναι 14,130 εκ²

8. Ο τροχός του ποδηλάτου έχει ακτίνα 14 cm. Προσδιορίστε την επιφάνεια του τροχού ποδηλάτου!

Απάντηση:

L = 4πr²

= 4 x 22/7 x 14²

= 2464

Έτσι, η επιφάνεια των τροχών του ποδηλάτου των οποίων οι ακτίνες είναι 14 cm 2464 εκ²

Αυτή είναι η συζήτηση σχετικά με τον τύπο για το χώρο του κτιρίου (εμβαδόν επιφανείας και όγκος κάθε χώρου του κτιρίου) που είναι πλήρης με προβλήματα δειγμάτων και συζήτηση. Ας ελπίσουμε ότι είναι χρήσιμο και κατανοητό!