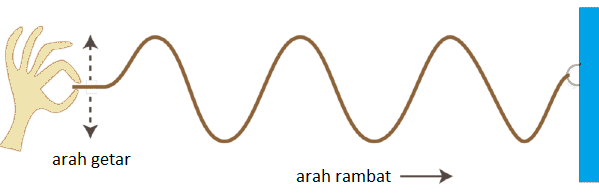
Formules GLBB et GLB avec des exemples de problèmes et de discussions
Nous savons certainement entendresignifie GLBB et GLB. Ouais! les deux sont du matériel que nous apprenons à l'école sur la physique. Où GLBB est un mouvement irrégulièrement rectiligne et GLB est un mouvement irrégulièrement rectiligne.
Dans la vie de tous les jours, l'application des deuxnous avons également vécu comme lorsque nous roulons à vélo sur une route en descente, il s'avère que c'est un exemple de GLBB et lorsqu'un train roule à vitesse constante qui est un exemple de GLB.
Cet article présentera les formules GLBB et GLB avec des exemples de problèmes et une discussion. Voici l'explication!
Formule GLBB
Si des changements dans la vitesse des objets se produisent régulièrement et que le chemin parcouru est une trajectoire rectiligne, alors le mouvement de l'objet est appelé "mouvement rectiligne changeant irrégulièrement".
Parce que les changements de vitesse subis par les objetsordonné, en d'autres termes, le mouvement en ligne droite change de façon irrégulière est un mouvement sur une trajectoire droite avec une accélération constante. De cette relation de vitesse et d'accélération, nous pouvons dériver la formule pour que la vitesse en mouvement droit change de manière irrégulière, qui est la suivante.

en prenant t0 = 0, alors:
Description:
v = vitesse finale
v0= vitesse initiale
a = accélération (fixe)
t = temps pris
De plus, nous pouvons également déterminer l'équation du déplacement (x) changement de mouvement rectiligne de manière irrégulière sur la base du graphique suivant.


Parce que v = v0+ à, puis:
Équations pour des cas plus généraux, où x0 = déplacement / position initiale.
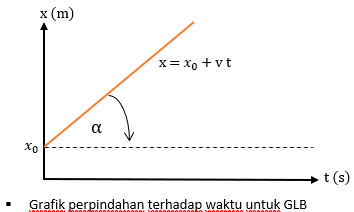
Le graphique du déplacement par rapport au temps peut donc être décrit comme suit.

Eh bien, basé sur l'équation x = x0 + v0t + 1/2 à2 et v = v0+ à, nous pouvons déterminer la relation entre la vitesse, l'accélération et le déplacement pour GLBB comme suit.
Si le transfert initial, x0 = 0, alors:
Formule GLB
Quand un objet parcourt la même distanceau même intervalle de temps à travers un chemin rectiligne, alors le mouvement de cet objet est appelé "mouvement rectiligne irrégulier". Dans ce cas, l'objet a une vitesse fixe (vitesse), alors son accélération est nulle.
Cette façon de trouver la distance peut être formulée comme suit:
s = v x t
Description:
s: distance (m ou km)
v: vitesse (m / s ou km / heure)
t: temps (seconde ou heure)
De cette façon, le graphique de vitesse en fonction du temps de ce mouvement se présente sous la forme d'une ligne droite horizontale comme celle-ci.

Ensuite, le déplacement peut être formulé avec une zone de ABCD, à savoir:
x = (t1-0) x (v0- 0)
En prenant des notes t1-0 = t et v0- 0 = v, puis:
x = v x t
Description:
x = mouvement d'objet (m ou km)
v = vitesse (m / s ou km / h)
t = temps de trajet (seconde ou heure)
De la formule ci-dessus, nous pouvons savoir que dans un mouvement uniforme droit, la distance et le mouvement des objets sont les mêmes, où s = v x t et x = v x t.
Alors que le graphique du déplacement par rapport au temps pour ce mouvement où x0 est la position initiale, qui est la suivante.
Exemples de questions et de discussions sur le GLBB et le GLB
1. Une voiture se déplace en ligne droite avec une vitesse fixe de 50 km / heure. Quelle est la distance parcourue par la voiture après 5 heures?
Discussion:
v = 50 km / heure
t = 5 heures
Répondu:
s = v x t
s = 50 km / h x 5 heures
s = 250 km
Ainsi, la distance parcourue en voiture après 5 heures est de 250 km.
2. Les trains qui se déplacent régulièrement en ligne droite peuvent parcourir une distance de 35 m pendant 0,05 seconde. Quelle est la vitesse du train?
Discussion:
s = 35 m
t = 0,05 s
Répondu:
v = s / t
v = 35 m / 0,05 s
v = 700 m / s
Ainsi, la vitesse du train est de 700 m / s
3. Le déplacement initial d'un objet se déplaçant à une vitesse fixe de 6 m / s est de -12 m. Quand l'objet a-t-il atteint le point avec le déplacement de 12 m?
Discussion:
x = 12 m
x0 = -12m
v = 6 m / s
Répondu:
x = x0+ v x t
12 m / s = -12 m / s + 6 t
6 t = 12 m / s + 12 m / s
t = 24 m / s: 6 s
t = 4 s
Ainsi, l'objet atteint un point avec un déplacement de 12 m / s soit en 4 s.
4. Miyako est à 40 m de la porte de l'école. Il conduit une moto à une vitesse de 30 m / s de la porte de l'école en 50 secondes. Calculez la position finale de Miyako et la distance parcourue par Miyako!
Discussion:
x0 = 40 m
v = 30 m / s
t = 50 s
Répondu:
x = x0 + v t
x = 40 m + (30 m / s x 50 s)
x = 40 m + 1 500 m
x = 1 540 m

Donc, la distance que Miyako parcourt est s = x - x0 = 1 540 m - 40 m = 1 500 m ou s = v x t = 30 m / s x 50 s = 1500 m.
5. Une voiture se déplace en ligne droite avec une vitesse fixe de 40 m / s pendant 30 secondes. Quelle est la distance parcourue par la voiture pendant cette période?
Discussion:
x0 = 0
v = 40 m / s
t = 30 s
Répondu:
x = x0 + v t
x = 0 + (40 m / s x 30 s)
x = 1 200 m
Distance parcourue peut-on trouver par la formule s = x - x0 = 1 200 m - 0 = 1 200 m.
Maintenant, à partir de ce qui précède, il peut prouver qu'en mouvement rectiligne régulier, la distance et le déplacement ont la même valeur.
6. Une voiture en marche droite est accélérée à vitesse régulière avec une vitesse initiale de 35 m / s. Après 15 secondes, la vitesse devient 50 m / s. Calculez l'accélération! (t0= 0)
Discussion:
v0 = 35 m / s
t0 = 0
v = 50 m / s
t = 15 s
Répondu:

7. Une particule se déplace avec une accélération fixe de 4 m / s2. Après un déplacement de 8 secondes, la vitesse des particules devient 400 m / s. Déterminez la vitesse initiale de la particule!
Discussion:
a = 4 m / s2
t = 8 s
v0 = 400 m / s
Répondu:
v = v0+ à
400 m / s = v0 + (4 m / s2 x 8 s)
400 m / s = v0 + 32 m / s
v0 = 400 m / s - 32 m / s
v0 = 368 m / s
8. Un objet se déplace à une vitesse initiale de 2 m / s. Après avoir bougé pendant 8 secondes, la vitesse de l'objet devient 10 m / s. Quel est le déplacement parcouru par l'objet pendant ce temps?
Discussion:
v0 = 2 m / s
v = 10 m / s
t = 8 s
Répondu:
x = (v + v0) x 1/2 t
x = (10 m / s + 2 m / s) x (1/2 x 8 s)
x = 12 m / s x 4 s
x = 48 m
9. Une voiture a une vitesse initiale de 3 m / s. Lorsque le déplacement augmente de 10 m, la vitesse devient 5 m / s. Quelle est l'accélération de la voiture?
Discussion:
v0 = 3 m / s
x = 10 m
v = 5 m / s
Répondu:
v2 = v02 + 2 haches
52 = 32 + (2 x a x 10)
25 = 9 + 20 a
20 a = 25 - 9
a = 16/20
a = 0,8 m / s2
10. Un avion atterrit à 150 m / s. Freine jusqu'à ce qu'il s'arrête dans les 20 secondes. Quelle est l'accélération et la distance?
Discussion:
v = 0
v0 = 150 m / s
t = 20 s
Répondu:
v = v0 + a t
0 = 150 m / s + (a x 20)
0 = 150 + 20a
-150 = 20a
a = -150/20
a = - 7,5 m / s2
Un signe négatif indique que l'accélération est ralentie.
Ainsi, la distance parcourue dans le déplacement est:
v2= v02 + 2a ∆x
02 = (1502) + 2 (-7,5) ∆x
0 = 22 500 - 15 ∆x
15 ∆x = 22 500
∆x = 22 500/15
∆x = 1 500 m
C'est toute la discussion cette fois sur les formules GLBB et GLB avec des exemples de problèmes et d'explications. J'espère que c'est utile!