Formules arithmétiques et géométriques avec des exemples de questions et leur discussion
Cet article abordera les formules arithmétiques et géométriques ainsi que des exemples de questions et leur discussion.
L'arithmétique et la géométrie sont nos thèmesapprendre à l'école en mathématiques. Lorsque, lors des examens nationaux, des examens d'entrée au collège ou des examens de candidature, il y a souvent des questions sur les deux.
Non seulement cela, nous devons également être en mesure de distinguerentre des séquences et des lignes arithmétiques ou des séquences et des lignes géométriques, car les règles des séquences et des lignes peuvent nous aider à effectuer des calculs, tels que les intérêts bancaires, les augmentations de production et les profits / pertes pour une entreprise. D'accord, regardons l'explication suivante!
Formules arithmétiques
-
Ligne arithmétique

Regardez le tableau ci-dessus, observez comment la différence de nombres de notre gauche à notre droite? Et puis, observez la différence de nombres de haut en bas?
D'après les observations, nous constatons que la différence d'une ligne est toujours fixe. Par exemple de notre rangée de droite à notre gauche: 1, 2, 3, 4, 5 (la différence est de 1).
5 - 1 = 4; 4 - 1 = 3; 3 - 1 = 2; 2 - 1 = 1
Et de haut en bas: 1, 6, 11, 16 (différence 5).
16 - 5 = 11; 11 - 5 = 6; 6 - 5 = 1
De telles lignes sont appelées séquences arithmétiques.
La différence qui a une valeur fixe est appelée différent et est symbolisé par b. En général, on peut dire que si Un est la formule syllabiquen une séquence arithmétique, puis elle s'applique
b = Un - Un-1
Si le premier mandat (U.1) symbolisé par un et la différence est symbolisée par b, puis le terme formulen la séquence peut être dérivée comme suit.
U1= a
U2= U1 + b = a + b
U3= U2 + b = (a + b) + b = a + 2b
U4= U3 + b = (a + 2b) + b = a + 3b
U5= U4 + b = (a + 3b) + b = a + 4b
Ainsi, les termes peuvent être formulés pourn des rangs arithmétiques est
Un= a + (n - 1)b
Description:
Un= tribu àn
a = première syllabe
b = différent
n = de nombreuses tribus
-
Série arithmétique
Si les termes de séquence arithmétique sont additionnés, une séquence arithmétique sera obtenue. Par exemple U1, U2, U3, ……., Un sont des tribus de rangs arithmétiques, alors U1 + U2 + U3 + .... + Un appelé progression arithmétique. Série arithmétique de n écrit avec la notation Sn avec Un= a + (n - 1)b.
Ainsi, la formule générale de la progression arithmétique est
S.n= 1/2 n (a + Un)
S.n= 1/2 n (2a + (n - 1) b)
Description:
S.n= nombre de progressions arithmétiques
a = première syllabe
b = différent
Un= tribu àn
n = de nombreuses tribus
Déterminez le termen séquence arithmétique si la formule numérique est connue n la première tribu. Tribu àn peut être déterminé par la formule suivante.
Un = Sn - S.n-1
-
Tribu moyenne de la ligne Arisan ou arithmétique
Si vous connaissez la séquence arithmétique suivante: U1, U2, U3, ……., Un, avec de nombreuses tribus arithmétiques en marcheest impair, donc il y a un terme au milieu de la ligne qui divise la ligne en 2 parties égales. Supposons que le milieu de la séquence soit Ut. Donc, trouver le moyen terme est le suivant.

Description:
Ut= la tribu moyenne des rangs arithmétiques
a = première syllabe
Un= dernière tribu de rangs arithmétiques avec de nombreux n bizarre
-
Insérer dans une ligne arithmétique
Par exemple U1, U2, U3, ……., Un, est une séquence arithmétique avec une syllabe initiale U1. Si entre deux termes consécutifs insérés k des nombres tels que de nouvelles séquences arithmétiques sont formées, les différentes nouvelles séquences arithmétiques sont formées comme suit.
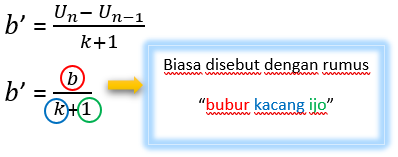
Description:
b ’= nouvelle différence après les insertions
b = différent avant les insertions
k = numéro inséré
Formules de géométrie
-
Ligne de géométrie
Essayez d'observer les rangées 1, 2, 4, 8, 16, .... Voyez que le terme suivant est obtenu en multipliant 2 dans le terme précédent. Cette séquence comprend la séquence géométrique.
Donc, on peut conclure en général, séquence géométrique est une séquence de nombres de chaque tribu obtenue à partir du terme précédent multipliée par un nombre constant (constant). Ces nombres fixes sont appelés ratio (comparaison) et symbolisé par r.
Si U1, U2, U3, U4......., Un séquence géométrique avec Un est la formule pourn, et ratio r, applicable:
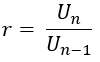
Formule générale pour la tribun séquence géométrique avec premier terme (U1) est déclaré un et ratio r, peut être dérivée comme suit.
U1= a
U2= U1 x r = ar
U3= U2 x r = ar²
U4= U3 x r = ar3
::
Un= Un-1 x r = arn-2 x r = arn-1
Séquence géométrique ainsi obtenue a, ar, ar², ...., arn-1.
Ainsi, la formule générale de lan la séquence géométrique est
Un= arn-1
Description:
Un = tribu àn
a = première syllabe
r = rapport
n = de nombreuses tribus
-
Série de géométrie
Si U1, U2, U3, U4......., Un est une rangée de géométrie alors U1 + U2 + U3+ U4 + …… .. Un est un série de géométrie avec Un = arn-1.
Formule générale de détermination des montants n le premier terme de la séquence géométrique peut être dérivé comme suit.
Par exemple S.n notation des montants n première syllabe.
S.n = U1 + U2 + U3 + …… .. Un
S.n = un + ar + ar2 + ... + arn-1…………………………………………………………………(1)
Si les deux segments sont multipliés r, alors
rSn = ar + ar2 + ar3 + ... + arn………………………………………………………………(2)
À partir de la différence dans les équations (1) et (2), nous pouvons obtenir

Donc, la formule de somme n le premier terme de la séquence géométrique, qui est le suivant.

Description:
S.n = le montant n première syllabe
a = première syllabe
r = rapport
n = de nombreuses tribus
-
Tribu centrale de la série Line ou Geometry
Par exemple, connaissez la séquence géométrique suivante: U1, U2, U3, U4......., Un (le nombre de termes est impair). Le terme moyen de la ligne est Ut, alors la formule est la suivante.
Description:
Ut= séquence géométrique à moyen terme
a = première syllabe
Un= la dernière séquence géométrique terme avec nombre n bizarre
-
Insérer dans la ligne de géométrie
Si dans la ligne de géométrie est insérée k les nombres de telle manière entre deux termes consécutifs, de sorte que de nouvelles lignes géométriques se forment. Ainsi, en trouvant le nouveau rapport peut être formulé comme suit.

Description:
r ’= nouveau rapport après insertion
r = rapport avant l'insertion
k = numéro inséré

-
Série de géométrie illimitée
Une série de géométrie infinie est une série géométrique qui ne peut pas être découpée par beaucoup de ses tribus. Prenons l'exemple suivant!
a. 1 + 2 + 4 + 8 + ...
b. 5 - 10 + 20 - 40 + ...
c. 1 + 1/2 + 1/4 + 1/8 + ...
d. 9 - 3 + 1 - 1/3 + ...
La série ci-dessus est un exemple de série de géométrie infinie. Considérez les exemples a et b. La série est séries divergentes, c'est-à-dire une série qui ne va pas à une certaine valeur et a un rapport r avec | r | > 1.
Ensuite, les exemples c et d sont série convergente, c'est-à-dire une série qui va à une certaine valeur et a un rapport r avec | r | <1.
Dans les séries convergentes, le nombre de termes ne dépassera pas un certain prix, mais approchera d'un certain prix. Ce prix particulier est appelé nombre infini de termes qui est noté S∞. Valeur S∞ représente la valeur d'approche (limite) de tout le terme (Sn) avec n approchant de l'infini. Par conséquent, la formule de série infinie peut être dérivée de la série géométrique avec le premier terme a, et n → ∞.

Parce que la série converge (| r | <1), pour n → ∞, alors arn→ 0 pour que

Ainsi, la formule du nombre de séries géométriques infinies est
Exemples de questions et discussion
1. Déterminez les 6e et 10e termes des rangées -3, 2, 7, 12, ...
Discussion:
un = -3
b = Un Un-1 = 2 - (-3) = 5
Un = a + (n-1) b, puis:
U6 = (-3) + (6-1) 5 = 22
U10 = (-3) + (10-1) 5 = 42
2. Trouvez les 90 premiers termes de la série 2 + 4 + 6 + 8 +
Discussion:
un = 2
b = 4-2 = 2
n = 90
alors,
S.n= 1/2n (2un + (n-1)b)
S.n= 1/2 x 90 (2 (2) + (90-1) 2)
S.n= 45 (4 + 178)
S.n= 45 (182)
S.n= 8 190
Les 90 premiers termes de la série sont donc 8 190.
3. Séquence arithmétique 3, 5, 7, 9, .... 1 007 sont connus.
Déterminez le terme moyen de la ligne.
Discussion:
a = 3
b = 5-7 = 2
Un = 1007, alors:
Ut = 1/2 (un + Un)
Ut = 1/2 (3 + 1007)
Ut = 1/2 (1 010)
Ut = 505
4. Lignes connues 2, 12, 22, 32, .... Entre deux termes successifs, 4 nombres sont insérés de telle manière qu'une nouvelle séquence arithmétique se forme. Déterminez:
une. Une nouvelle différence
b. Formule du nième terme
c. Le premier nombre n termes de la nouvelle séquence arithmétique.
Discussion:
a.

b. La formule du nième terme est
Un = a + (n-1) b
Un = 2 + (n-1) 2
Un = 2 + (2n-2)
Un = 2n
c. Le numéro du premier terme n est
S.n= 1/2n (un + Un )
S.n= 1/2n (2 + 2n)
S.n= n (n + 1)
5. Trouvez le premier terme, le rapport et le 8e terme de la séquence géométrique 2, 6, 18, 54, ...
Discussion:
a = 2
r = U2/ U1 = 6/2 = 3
alors,
Un= arn-1
U8= ar8-1
U8= 2 (38-1)
U8= 2 (37)
U8= 2 (2 187)
U8= 4 374
6. Déterminez le nombre de séries géométriques 2 + 4 + 8 + 16 + ... (8 tribus)
Discussion:
un = 2
r = U2/ U1 = 4/2 = 2 (r> 1)
Le nombre de lignes jusqu'aux 8 premiers termes est significatif n = 8

Ainsi, les 8 premiers termes de la série géométrique sont 510.
7. Les rangées de géométrie sont connues 1/8, 1/4, 1/2, 1, 2, 4, .... 2048. Déterminez le terme moyen de la ligne.
Discussion:
a = 1/8
r = U2/ U1 = 1/8: 1/4 = 2
Un = 2 048
alors,
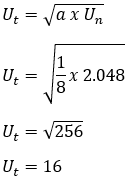
8. On sait que la séquence géométrique est 1/32, 1/16, 1/8, 1/4, .... Entre deux termes successifs, trois nombres sont insérés de telle manière qu'une nouvelle séquence géométrique se forme. Déterminer:
a. Rapport positif des nouvelles lignes géométriques
b. La formule du nième terme de la nouvelle séquence géométrique
c. Le premier nombre n termes de la nouvelle ligne de géométrie.
Discussion:
Séquence géométrique 1/32, 1/16, 1/8, 1/4, ... ou peut également être servi 2-5, 2 -4, 2-3, 2-2, ....
a. Considérons deux termes consécutifs, par exemple U1 et U2 = 1/32 et 1/16, puis:

b. La formule du nième terme est
Un= arn-1
Un= 2-5(2n / 4-1)
Un= 2n / 4-6
c. Le montant n le premier terme est

9. Déterminer le nombre infini de termes de la série géométrique 1 + 1/2 + 1/4 + 1/8 + ...
Discussion:
a = 1
r = U2/ U1 = 1/2: 1 = 1/2
alors,

10. Le premier terme d'une série de géométries est 2 et la somme à l'infini est 4. Trouvez le rapport.
Discussion:
a = 2
S.∞ = 4
on substitue ensuite la formule S∞
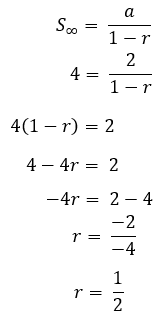
C'est l'explication des formules arithmétiques et géométriques ainsi que des exemples de questions et leur discussion. J'espère que c'est utile!








