क्यूब्स के वॉल्यूम के लिए फॉर्मूला और क्यूब्स के सरफेस एरिया और समस्याओं के उदाहरण
पहले हमने सूत्रों के बारे में चर्चा की हैट्यूब की मात्रा, अच्छी तरह से फिर भी निर्माण स्थान के बारे में चर्चा करते हुए, इस बार घन की मात्रा खोजने के सूत्र पर चर्चा करेंगे। क्यूब एक ऐसी इमारत है जिसमें समान लंबाई के 12 फलों की पसलियां होती हैं और इसमें 6 भुजाएँ होती हैं जिन्हें एक वर्ग के आकार का बनाया जाता है
क्यूब में आमतौर पर भागों होते हैं, अर्थात्: समतल, रिब, विकर्ण तल, शीर्ष, विकर्ण पक्ष और विकर्ण स्थान। इसी तरह, अन्य क्यूब्स में एक वॉल्यूम है लोह। अधिक जानकारी के लिए, नीचे दिए गए स्पष्टीकरण पर विचार करें!
घन आयतन सूत्र
किसी घन की मात्रा पर चर्चा करने से पहले हम पहले इसकी मात्रा से संबंधित तत्वों पर चर्चा करते हैं।
- क्षेत्र / पक्ष
घन का क्षेत्रफल / पक्ष कुछ ऐसा है जो घन में एक सीमा है। ठीक है, क्यूब के 6 पक्ष हैं जिनकी लंबाई एक वर्ग के आकार में है।
क्यूब के किनारे का हिस्सा:
- ऊपरी तरफ (EFGH)
- निचला पक्ष (ABCD)
- सामने की ओर (ABFE)
- पीछे की तरफ (DCGH)
- दाईं ओर (ADHE)
- लेफ्ट साइड साइड (BCGF)
- पार्श्व
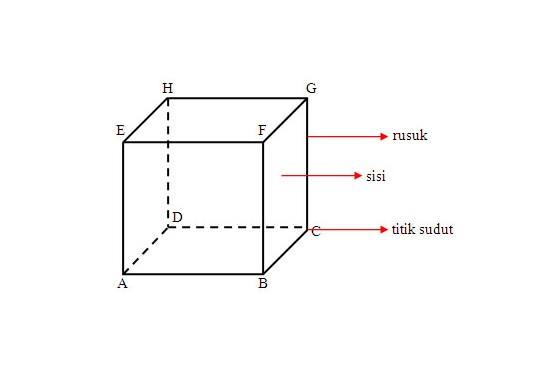
पीडीए क्यूब लाइनों कि 2 क्षेत्रों / पक्षों के बीच चौराहों को पसलियों कहा जाता है। ऊपर की तस्वीर में, क्यूब रिब सहित एबी, एई, बीसी, बीएफ, सीडी, सीजी, डीए, डीएच, ईएफ, एचई, एफजी, जीएच हैं।
- शिखर
घन में 2 या 3 पसलियों के बीच के चौराहे के बिंदु को सुडुर बिंदु कहा जाता है। क्यूब के ऊपर की तस्वीर के आधार पर 8 कोण होते हैं जैसे A, B, C, D, E, F, G, H।
- विकर्ण पक्ष / विकर्ण विमान
अगर हर कोने पर लंबी लाइन दी जाएसामना करने वाला घन एक समान त्रिभुज के रूप में बनेगा। रेखा एक विकर्ण पक्ष या विमान है। ऊपर क्यूब की तस्वीर के आधार पर 12 विकर्ण पक्ष / क्षेत्र हैं जैसे एसी, एएफ, एएच, बीडी, बीई, बीजी, सीएच, डीई, डीजी, ईजी, एफसी, और एचजी।
- विकर्ण स्थान
एक स्थान में एक रेखा बन जाती हैएक दूसरे के सामने दो बिंदुओं के बीच जुड़ने को अंतरिक्ष का विकर्ण कहा जाता है। ऊपर के क्यूब के चित्र के आधार पर 4 विकर्ण रिक्त स्थान हैं, जैसे एजी, बीएच, डीएफ, और ईसी लाइनें।
- विकर्ण विमान
2 रेखाओं से बना एक क्षेत्रविकर्ण पक्ष / विमान और 2 समानांतर पसलियों को विकर्ण विमान कहा जाता है। ऊपर क्यूब की छवि के आधार पर 4 विकर्ण क्षेत्र हैं जैसे कि ABGH, ACGE, DBFH, EFCG।
अच्छी तरह से, अगले क्यूब को पहचानने के बाद हम वॉल्यूम को खोजने के सूत्र पर चर्चा करते हैं हाँ। नीचे दिए गए सूत्र पर विचार करें:

उदाहरण प्रश्न और चर्चा
निम्नलिखित समाप्त ट्यूबों की मात्रा से संबंधित कुछ प्रश्न बताएंगे चलो ध्यान से देखा तो आप समझ गए!
1. 15 सेमी लंबी पसलियों के साथ एक घन। घन की मात्रा की गणना करें!
उत्तर:
s = 15 सेमी
नली का आयतन
- वी = एस3
- = 15 सेमी x 15 सेमी x 15 सेमी
- = 3375 सेमी3
इस प्रकार, घन का आयतन है 3375 सेमी3
2. यदि घन का आयतन 343 सेमी है3, क्यूब की लंबाई क्या है?
उत्तर:
वी = 343 सेमी3
- फिर, वी = एस3
- 343 सेमी3 = एस3
- s = 3343
- s = 7 सेमी
इस प्रकार, क्यूब की लंबाई होती है 7 सेमी पक्ष।
3. एक रुबिक में 5 सेमी का हिस्सा होता है। रुबिक का आयतन ज्ञात कीजिये?
उत्तर:
- वी = एस3
- = 5 सेमी x 5 सेमी x 5 सेमी
- = 125 सेमी3
इस प्रकार, रुबिक का आयतन है 125 से.मी.3
4. यदि ब्रेस की लंबाई 20 सेमी है। तिजोरी का आयतन क्या है?
उत्तर:
- V = साइड x साइड x साइड
वी = 20 सेमी x 20 सेमी x 20 सेमी
वी = 8000 सेमी3
इस प्रकार, तिजोरी का आयतन है 8000 से.मी.3
5. एक बाथटब में 2.5 सेंटीमीटर लंबी पसलियां होती हैं, जिससे टब में कितना पानी भर सकता है?
उत्तर:
- V = साइड x साइड x साइड
V = 2.5 m x 2.5 m x 2.5 m
वी = 15,625 मीटर3
इस प्रकार, बहुत पानी की जरूरत है ताकि एक पूर्ण बाथटब हो 15,625 मी3
6. क्यूब के आकार के बॉक्स की मात्रा 729 सेमी है3, गणना करें कि बॉक्स की समग्र रिब लंबाई क्या है?
उत्तर:
- वी = एस3
729 = एस3
s = 729
s = 29729
s = 9 सेमी
घन पसलियों की संख्या = 12
पसलियों की कुल संख्या = 9 x 12 = 108 सेमी
इस प्रकार, बॉक्स की पसलियों की समग्र लंबाई 108 सेमी।
7। एंडी ने 14 सेमी लंबी रिब के साथ एक क्यूब के आकार के बाथटब में पानी डाला। लेकिन एंडी द्वारा डाला गया पानी की मात्रा बेसिन का केवल आधा था। एंडी ने कितना पानी डाला है?
उत्तर:
स्नान में पानी की मात्रा = मात्रा water घन
टब में पानी की मात्रा = s x s3
= Cm x 14 सेमी x 14 सेमी x 14 सेमी
= 7 x 2,744 सेमी3
= 1,372 सेमी3
इस प्रकार, एंडी ने जितना पानी डाला है, वह है 1,372 सेमी3.
8. क्यूब की पसलियों की लंबाई 12 सेमी है। फिर एक छोटे आकार के साथ क्यूब्स में काट लें जो 3 सेमी लंबी पसलियों है। निर्धारित करें कि कितने छोटे क्यूब्स का उत्पादन किया जाता है?
उत्तर:
बड़े घन की मात्रा = 12 सेमी x 12 सेमी x 12 सेमी = 1,728 सेमी3
छोटे घन की मात्रा = 3 सेमी x 3 सेमी x 3 सेमी = 27 सेमी3
छोटे क्यूब्स की कुल संख्या = 1,728: 27 = 64
इस प्रकार, टुकड़ा करने के बाद सभी छोटे क्यूब्स का योग है 64 टुकड़े
9. राइबेज 24 सेमी लंबा होने पर एक घन का विकर्ण क्षेत्र क्या है? (डिक: =2 = 1,414)
उत्तर:
विकर्ण क्षेत्र का क्षेत्रफल = 24 सेमी x 24 सेमी x area2
= 10 सेमी x 10 सेमी x 1,414
= 814,464 सेमी2
इस प्रकार, विकर्ण का क्षेत्र है 814,464 सेमी2
10. 10 सेमी पसलियों के साथ एक क्यूब के आकार का बॉक्स, फिर 500 सेमी की मात्रा के साथ छोटे क्यूबिक बक्से में काट लें3 गणना करें कि आपके पास कुल कितने छोटे क्यूब्स हैं!
उत्तर:
बड़े बॉक्स (घन) = 10 सेमी x 10 सेमी x 10 सेमी = 1,000 सेमी की मात्रा3 </ सूप
छोटे घन का आयतन = 500 सेमी3 </ सूप
छोटे क्यूब्स की संख्या = बड़े क्यूब्स की मात्रा: छोटे क्यूब्स की मात्रा
छोटे क्यूब्स की संख्या = 1,000: 500 = 2 टुकड़े
इस प्रकार, टुकड़ा करने के बाद सभी छोटे क्यूब्स का योग है 2 टुकड़े
ठीक है, उम्मीद से ऊपर के सवालों और चर्चा सेआप आसानी से समझ सकते हैं कि क्यूब वेक फॉर्मूला से संबंधित होने पर समस्याओं को कैसे हल किया जाए। सादगी के लिए, आपको पहले सूत्र को याद करना होगा, फिर समस्या के उद्देश्य को समझना चाहिए और समस्या में क्या जाना जाता है।