सवालों के उदाहरणों और उनकी चर्चा के साथ त्रिकोणमिति सूत्रों का संग्रह
आप में से जो अभी भी एक छात्र हैंऔर जिन्होंने काम किया है उन्होंने गणित का अध्ययन किया होगा। यह विषय वास्तव में प्राथमिक विद्यालय के बाद से विश्वविद्यालय में छात्रों तक पढ़ाया गया है।
यहां तक कि गणित को हमेशा स्कूली परीक्षाओं और शिक्षा के कई स्तरों पर राष्ट्रीय परीक्षाओं में शामिल किया जाता है।
क्योंकि यह विषय भी छात्रों से भरा हुआ हैजो अक्सर शिकायत करता है कि उसे गणित की समस्याएं करने के लिए असाइनमेंट मिला है। दरअसल गणित के कुछ सूत्र दिमाग को समझने के लिए काफी हैं। एक गणितीय सूत्र जो सीखना बहुत कठिन है, वह त्रिकोणमितीय सूत्र है।
त्रिकोणमिति सूत्रों का संग्रह

त्रिकोणमिति सूत्रों की बात करें तो आपत्रिकोण आकृतियों के बारे में जानेंगे। क्योंकि त्रिकोणमिति सूत्र एक ऐसा सूत्र है जो त्रिभुज आकार में मौजूद कोणों और पक्षों के बीच संबंधों का अध्ययन करता है। जबकि त्रिकोणमितीय फ़ंक्शन स्वयं को तीन में विभाजित किया जाता है, अर्थात् व्यंजन (कोस), साइन (पाप), सेकान (सेकंड), स्पर्शरेखा (टैन), कॉटैंगेन (कोटन), और कोसेन (कोसेक)।
1. त्रिकोणमिति समारोह सूत्र
पहला त्रिकोणमितीय सूत्र ऊपर त्रिकोणमितीय कार्यों से आता है। जहां प्रत्येक सूत्र में त्रिकोण के प्रत्येक कोने से गणना करने का एक तरीका है। त्रिकोणमितीय फ़ंक्शन सूत्र है

सूत्र के लिए पाप α का उपयोग पक्षों की गणना करने के लिए किया जाता हैसामने की ओर से विभाजित भाग। जबकि सूत्र cos α का उपयोग कर्ण द्वारा विभाजित पक्ष की गणना करने के लिए किया जाता है। और तन α त्रिकोण में कर्ण के लिए सामने की ओर से सूत्र है। ऊपर दिए गए तीन सूत्र कार्यों को याद रखना आसान बनाने के लिए, आप निम्नलिखित संक्षिप्ताक्षरों का उपयोग कर सकते हैं।
SinDeMi
स्लोपिंग फ्रंट साइनस या पाप α फार्मूला की संक्षिप्तता।
CosSaMi
साइड स्लोपिंग कोसाइन या कॉस α फॉर्मूला।
TanDeSa
और संक्षिप्त नाम TanDeSa साइड फ्रंट टैंगेंट या टैन α सूत्र के लिए है।
2. त्रिकोणमिति पहचान सूत्र

त्रिकोणमितीय पहचान सूत्र एक सूत्र हैत्रिकोणमिति की तुलना x कोण चर से करें। जहां डिग्री और रेडियंस के माप से x चर प्राप्त किया जाता है। जबकि समीकरण को हल करने का तरीका पाप xº = पाप? ° (x? R) है:
पहले कोण अनुपात पाप (180º -? Sin) = पाप? Sin और पाप का उपयोग करें (? K + k.360?) = पाप? Sin। फिर समीकरण में प्रवेश करें पाप xº = पाप? Sin हो
यदि पाप x0 = पाप?0 (x? R), तब:
x = + k.3600 या x = (1800 ? ?) + k.360, k के साथ? बी
नोट: x डिग्री में है
यदि पाप x = पाप A (x? R) है, तो:
x = A + k.2? या x = (ए?) + k.2?, कश्मीर के साथ। बी
नोट: x रेडियन में है
3. त्रिकोणमिति कोण राशि और अंतर
त्रिकोणमिति में तीसरा सूत्र योग और त्रिकोणमितीय कोणों में अंतर का सूत्र है। सूत्र है:

इस सूत्र का उपयोग त्रिभुज के कोण और भुजाओं को जोड़ने के लिए किया जाता है।
4. त्रिकोणमिति गुणन सूत्र

त्रिकोण के कोण और पक्षों में गुणा के लिए, आप ऊपर त्रिकोणमितीय गुणन सूत्र का उपयोग कर सकते हैं।
5. त्रिकोणमिति राशि और अंतर सूत्र

त्रिभुज में न केवल जोड़ सूत्र होता है, बल्कि एक ऐसा पक्ष भी होता है जिसे एक ही समय में योग के लिए अंतर के लिए और ऊपर त्रिकोणमितीय अंतर के साथ अंतर की तलाश करनी चाहिए।
6. त्रिकोणमिति डबल और 3 कोण सूत्र

7. त्रिकोणमिति आधा कोण सूत्र

त्रिकोण पर गणना की जा सकने वाले कोण न केवल पूर्ण कोण हैं, बल्कि त्रिकोण के आधे कोणों की गणना त्रिकोणमितीय आधे-कोणों के सूत्र के साथ की जा सकती है।
8. त्रिकोणमिति विशेष कोण सूत्र

ऊपर दिए गए सात सूत्रों के अलावा, त्रिकोणमिति सूत्र में भी विशेष कोण हैं

इसलिए जब आप किसी समस्या पर काम कर रहे होंत्रिकोणमिति तब आपको पहले से पता लगाना होगा कि क्या समस्या सामान्य त्रिकोणमिति सूत्र के साथ या विशेष त्रिकोणमितीय सूत्र के साथ कोई समस्या है। क्योंकि आपके द्वारा उपयोग किया जाने वाला प्रत्येक सूत्र प्रश्नों के उत्तर देने में सटीकता के साथ-साथ विभिन्न परिणाम देगा।
त्रिकोणमिति के उदाहरण
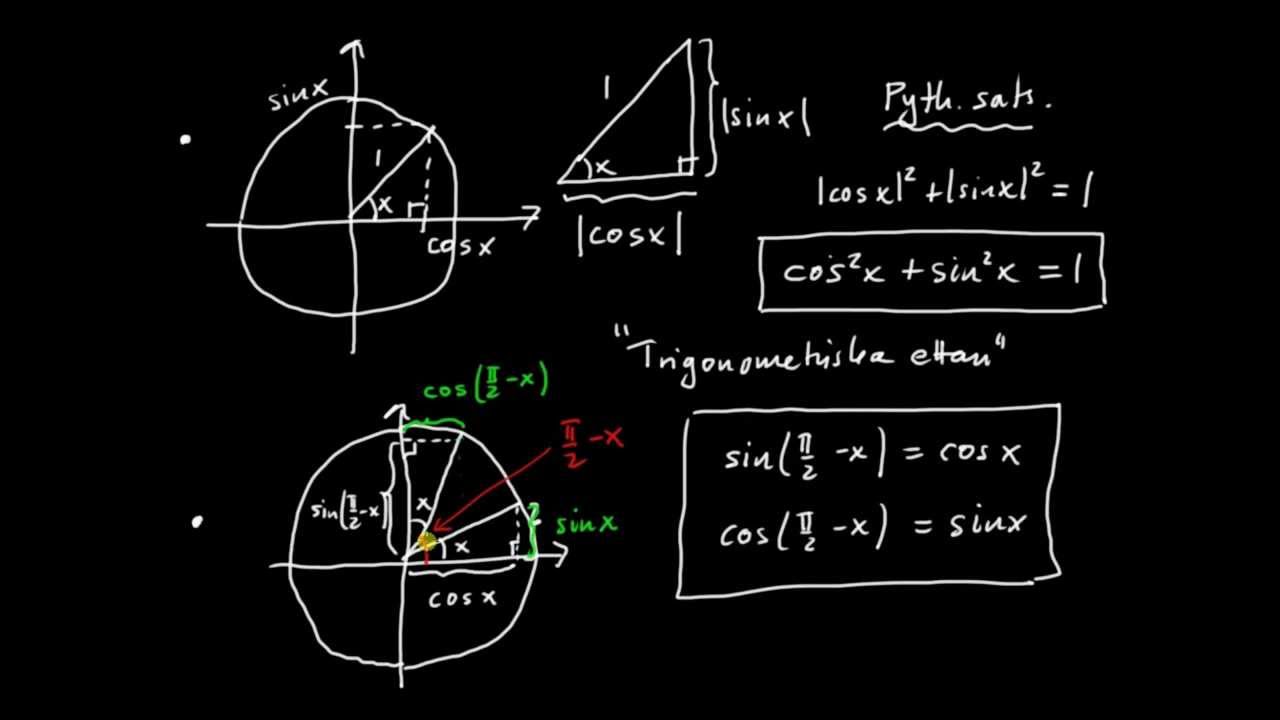
कैसे करें? क्या आप ऊपर त्रिकोणमितीय सूत्र के बारे में समझते हैं? दरअसल, सूत्र को समझना काफी मुश्किल है, लेकिन इसका मतलब यह नहीं है कि आप कोशिश करते रहें तो आप नहीं कर सकते। आप त्रिकोणमितीय समस्याओं के माध्यम से त्रिकोणमितीय सूत्रों को भी समझ सकते हैं। त्रिकोणमिति के बारे में प्रश्नों के कुछ उदाहरणों के लिए जिन्हें आप आज़मा सकते हैं:
1. पाप का मूल्य निर्धारित करें 105º + पाप 15 of
ऊपर त्रिकोणमितीय समस्या एक अतिरिक्त प्रकार की त्रिकोणमितीय समस्या है, इसलिए आप इसके अलावा त्रिकोणमितीय सूत्र का उपयोग कर सकते हैं जो 2 पाप B (A + B) cos ½ (A-B) है। प्रक्रिया है:
पाप का मान 105 ° + पाप 15 ° = 2 पाप 105 (105 + 15) ° cos ½ (105-15) °
= 2 पाप 90 (102) ° cos sin (90) °
= पाप 60 ° cos 45 °
तो समस्या पाप 105º + पाप 15 sin का उत्तर पाप 60º cos 45 problem है।
2. पाप xº पाप 25 the का समीकरण मान ज्ञात कीजिए
उपरोक्त प्रश्नों का निपटान, अर्थात्:
x = 250 + k.3600 या x = (1800 ? 250) + के .3600
= 1550 + k.3600
तो, x = 250 + k.3600 या 155 or + k.3600
तो पाप xº पाप 25º का समीकरण मान x = 25 है0 + k.3600 या 155 or + k.3600.
3. गुणन 2 cos 75º cos 15 of का मान ज्ञात कीजिए
तीसरी समस्या त्रिकोणमितीय गुणन मॉडल के ऊपर है। प्रयुक्त सूत्र 2 cos A cos B = cos (A + B) + cos (A-B) है। समस्या का हल है:
2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75 - 15) °
= cos 90 ° + cos 60 °
= 0 + ½
= ½
तो 2 cos 75º cos 15½ को गुणा करने का परिणाम lying है।
4. ए त्रिभुज ABC तीक्ष्ण बिंदु, ज्ञात cos A = 4/5 और sin B = 12/13 है, तो पाप C है ...
क्योंकि त्रिभुज ABC में एक तीव्र कोण है, तो कोण A, B और C भी तीव्र हैं, इसलिए:
cos A = 4/5, फिर पाप A = 3/5,
पाप B = 12/13, फिर cos B = 5/13
A + B + C = 180 °, (एक त्रिभुज में कोणों की संख्या = 180)
ए + बी = 180 - सी
पाप (A + B) = पाप (180 - C)
पाप ए। cos B + cos A.sin B = sin C, (परस्पर संबंधित त्रिभुजों का कोण: sin (180-x) (sin x))
sin C = sin A.cos B + cos A.sin B
पाप C = 3 / 5.5 / 13 + 4 / 5.12 / 13
पाप C = 15/65 + 48/65 = 63/65
उपरोक्त सूत्र से, पाप C मान 63/65 है
5. तय करें पाप 120 का मानओ
प्रश्न संख्या 5 के लिए इसे काम करने के दो तरीके हैं। पहला तरीका है:
120 = 90 + 30
तो पाप 120ओ सूत्र पाप 120 के साथ गणना की जा सकती हैओ = पाप (90)ओ + 30ओ) = कॉस 30ओ (एक सकारात्मक मूल्य प्राप्त किया क्योंकि 120º चतुर्थांश II (2) में है, इसलिए परिणाम भी सकारात्मक है)
कॉस 30ओ = √ √3
या दूसरे तरीके से, अर्थात्:
180 के समानओ-80º
पाप 120ओ = पाप (१ (०)ओ - 60ओ) = पाप ६०ओ = √ √3
तो पाप 120º का परिणाम º º3 है।
6. ए एबीसी त्रिकोण की साइड लंबाई एबी = 6 सेमी, बीसी = 8 सेमी एसी = 7 सेमी है। Cos A का मान है ।।
उपरोक्त समस्या को सूत्र के साथ कैसे करें:
कॉस ए = (एबी² + एसी²-बीसी () / २ (एबी एसी)
Cos A = 6 (+ 7²-8² / 2 (6. 7)
कॉस ए = 36 + 49-64 / 2 (42)
कॉस ए = 21/84
ताकि कॉस ए 21/84 पाया जाए।
7. पॉइंट पी और क्यू को ध्रुवीय निर्देशांक का उपयोग करके व्यक्त किया जाता है। फिर अंक P और Q के बीच की दूरी निर्धारित करें!

उपरोक्त समस्या के लिए, कॉन्सिनस सूत्र का उपयोग करें, जो है:
कोण POQ = 180 की मात्राओ - (75)ओ+45ओ) = 60ओ.
पीक्यू2 = ओक्यू2 + ओपी2 - 2.OQ.OP cos ∠POQ
पीक्यू2 = ३2 + ५2 - 2.3.5 cos 60ओ ग
पीक्यू2 = 9 + 25 - 30. 0.5
पीक्यू2 = 9 + 25 -15
पीक्यू2 = 19
पीक्यू = Q19 = 4.36
फिर P और Q के बीच की दूरी 4.36 है।
अब, त्रिकोणमितीय सूत्रों और समस्या के उदाहरणों के बारे में कुछ चर्चा हुई। आशा है कि यह आपके लिए उपयोगी है।








