Aritmetičke i geometrijske formule s primjerima pitanja i njihovom raspravom
U ovom će se članku raspravljati o aritmetičkim i geometrijskim formulama, uz primjere pitanja i njihovu raspravu.
Aritmetika i geometrija su naše temeučiti u školi matematiku. Tamo gdje su državni ispiti, prijemni ispiti na fakultetu ili ispiti za prijavu na posao često se postavljaju pitanja o oba.
I ne samo to, moramo i moći razlikovatiizmeđu aritmetičkih nizova i redaka ili geometrijskih nizova i redaka, jer nam pravila sekvence i redaka mogu olakšati dovršavanje izračuna, poput bankarskih kamata, povećanja proizvodnje i dobiti / gubitka za posao. U redu, pogledajmo sljedeće objašnjenje!
Aritmetičke formule
-
Aritmetički red

Pogledajte gornju tablicu, promatrajte kako je razlika u brojevima s naše lijeve na desnu stranu? I onda, promatrajte razliku u brojevima od vrha do dna?
Iz opažanja nalazimo da je razlika iz jedne crte uvijek fiksna. Na primjer, iz desnog retka s naše lijeve strane: 1, 2, 3, 4, 5 (razlika je 1).
5 - 1 = 4; 4 - 1 = 3; 3 - 1 = 2; 2 - 1 = 1
I od vrha do dna: 1, 6, 11, 16 (razlika 5).
16 - 5 = 11; 11 - 5 = 6; 6 - 5 = 1
Ovakvi redovi se nazivaju aritmetičkim nizovima.
Razlika koja ima fiksnu vrijednost naziva se razlika a simbolizira ga b. Općenito se može reći da ako Un je formula slogan aritmetički niz, tada se primjenjuje
b = Un - Un-1
Ako prvi pojam (U1) simbolizirali jedan a razlika simbolizira s B, zatim termin formulan slijed se može izvesti na sljedeći način.
U1= a
U2= U1 + b = a + B
U3= U2 + b = (a + b) + b = a + 2b
U4= U3 + b = (a + 2b) + b = a + 3b
U5= U4 + b = (a + 3b) + b = a + 4b
Dakle, izrazi se mogu formulirati un aritmetičkih redova je
Un= a + (n - 1)B
primjedbe:
Un= pleme don
a = prvi slog
b = razlika
n = mnoga plemena
-
Aritmetička serija
Ako se izrazi aritmetičkih nizova zbroje, dobit će se aritmetička sekvenca. Na primjer U1, U2, U3, ……., Un su plemena aritmetičkih redova, dakle U1 + U2 + U3 + .... + Un zvao aritmetička progresija. Aritmetička serija iz n napisana S notacijomn s Un= a + (n - 1)b.
Dakle, opća formula za aritmetičku progresiju je
Sn= 1/2 n (a + U)n)
Sn= 1/2 n (2a + (n - 1) b)
primjedbe:
Sn= broj aritmetičkih napredovanja
a = prvi slog
b = razlika
Un= pleme don
n = mnoga plemena
Odredite termin don aritmetički niz ako je poznata formula broja n prvo pleme. Pleme don može se odrediti sljedećom formulom.
Un = Sn - Sn-1
-
Srednje pleme arijske linije ili aritmetike
Ako znate sljedeći aritmetički niz: U1, U2, U3, ……., Un, s mnogim aritmetičkim marširajućim plemenimaneparno je, pa postoji izraz desno u sredini crte koji liniju dijeli na 2 jednaka dijela. Pretpostavimo da je srednji pojam niza Ut, Dakle, pronaći srednji pojam je sljedeći.

primjedbe:
Ut= srednje pleme aritmetičkih redova
a = prvi slog
Un= posljednje plemstvo aritmetičkih redova s mnogima n neparan
-
Umetnite u Aritmetički red
Na primjer U1, U2, U3, ……., Un, je aritmetička sekvenca s početnim slogom U1. Ako su umetnuta dva uzastopna termina k brojevi takvi da nastaju nove aritmetičke sekvence, različiti novi aritmetički nizovi se formiraju kako slijedi.
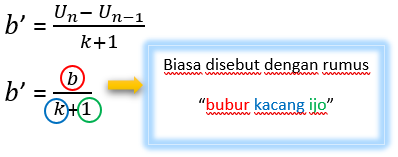
primjedbe:
b '= nova razlika nakon umetanja
b = prije umetanja
k = umetnuti broj
Formule geometrije
-
Linija geometrije
Pokušajte promatrati redove 1, 2, 4, 8, 16, .... Pogledajte da je sljedeći pojam dobiven množenjem 2 u prethodnom izrazu. Taj niz uključuje geometrijski niz.
Dakle, općenito se može zaključiti, geometrijski slijed je niz brojeva koje je svako pleme dobilo iz prethodnog izraza pomnoženo sa stalnim brojem (konstantom). Ti se fiksni brojevi nazivaju omjer (usporedba) i simbolizirali su ga r.
ako U1, U2, U3, U4......., Un geometrijski slijed sa Un je formula zan, i omjer r, primjenjuju se:
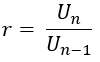
Opća formula za plemen geometrijski slijed s prvim pojmom (U1) proglašen je jedan i omjer r, može se izvesti na sljedeći način.
U1= a
U2= U1 x r = ar
U3= U2 x r = ar²
U4= U3 x r = ar3
::
Un= Un-1 x r = arn-2 x r = arn-1
Tako dobiven geometrijski slijed a, ar, ar², ...., arn-1.
Dakle, opća formula zan geometrijski slijed je
Un= arn-1
primjedbe:
Un = pleme don
a = prvi slog
r = omjer
n = mnoga plemena
-
Serija geometrije
ako U1, U2, U3, U4......., Un je red geometrije tada U1 + U2 + U3 + U4 + …… .. Un je a niz geometrija s Un = arn-1.
Opća formula za određivanje iznosa n prvi pojam geometrijskog niza može se izvesti na sljedeći način.
Na primjer Sn notacija iznosa n prvi slog.
Sn = U1 + U2 + U3 + …… .. Un
Sn = jedan + ar + ar2 + ... .. + arn-1...........................................................................(1)
Ako se množe oba segmenta r, tada
RSn = ar + ar2 + ar3 + ... .. + arn........................................................................(2)
Iz razlike u jednadžbama (1) i (2) možemo dobiti

Dakle, formula zbroja n prvi pojam niza geometrija, koji je sljedeći.

primjedbe:
Sn = iznos n prvi slog
a = prvi slog
r = omjer
n = mnoga plemena
-
Središnje pleme niza ili niz geometrija
Na primjer, znate sljedeći geometrijski red: U1, U2, U3, U4......., Un (broj izraza je neparan). Srednji pojam linije je Ut, onda je formula sljedeća.
primjedbe:
Ut= srednjoročni geometrijski niz
a = prvi slog
Un= geometrijski slijed posljednjeg termina s brojem n neparan
-
Umetnite u red geometrije
Ako je umetnut red geometrije k brojeve na takav način između dva uzastopna izraza, tako da se formiraju nove geometrijske crte. Dakle, u pronalaženju novog omjera može se formulirati na sljedeći način.

primjedbe:
r '= novi omjer nakon umetanja
r = omjer prije umetanja
k = umetnuti broj

-
Neograničena serija geometrije
Beskonačni niz geometrija je geometrijski niz koji mnoga plemena ne mogu sjeći. Razmotrite sljedeći primjer!
a. 1 + 2 + 4 + 8 + ...
b. 5 - 10 + 20 - 40 + ...
c. 1 + 1/2 + 1/4 + 1/8 + ...
d. 9 - 3 + 1 - 1/3 + ...
Gornja serija primjer je beskonačnog niza geometrije. Razmotrimo primjere a i b. Serija je divergentne serije, tj. niz koji ne ide do određene vrijednosti i ima omjer r s | r | > 1.
Zatim su primjeri c i d konvergentni niz, tj. niz koji ide do određene vrijednosti i ima omjer r s | r | <1.
U konvergentnim serijama broj pojmova neće premašiti određenu cijenu, već će se približiti određenoj cijeni. Ta posebna cijena se zove beskonačan broj pojmova koji je označen sa S∞. S vrijednost∞ predstavlja pristupnu vrijednost (granicu) cijelog pojma (Sn) sa n približavajući se beskonačnosti. Stoga se formula beskonačnog niza može izvesti iz geometrijskih serija s prvim pojmom a, i n → ∞.

Jer se serija konvergira (| r | <1), za n → ∞, tada arn→ 0 tako da

Dakle, formula za broj beskonačnih geometrijskih serija je
Primjer pitanja i rasprava
1. Odredite 6. i 10. pojave redaka -3, 2, 7, 12, ...
rasprava:
jedan = -3
B = Un - Un-1 = 2 - (-3) = 5
Un = a + (n-1) b, tada je:
U6 = (-3) + (6-1) 5 = 22
U10 = (-3) + (10-1) 5 = 42
2. Pronađite prvih 90 pojmova iz serije 2 + 4 + 6 + 8 +
rasprava:
jedan = 2
B = 4 - 2 = 2
n = 90
zatim,
Sn= 1/2n (2jedan + (n-1)B)
Sn= 1/2 x 90 (2 (2) + (90-1) 2)
Sn= 45 (4 + 178)
Sn= 45 (182)
Sn= 8.190
Dakle, prvih 90 termina u seriji je 8.190.
3. Aritmetički niz 3, 5, 7, 9, .... poznati su 1.007.
Odredite srednji pojam pravca.
rasprava:
a = 3
b = 5-7 = 2
Un = 1.007, tada:
Ut = 1/2 (jedan + Un)
Ut = 1/2 (3 + 1.007)
Ut = 1/2 (1.010)
Ut = 505
4. Poznati redovi 2, 12, 22, 32, .... Između dva uzastopna izraza, 4 broja se umetnu na takav način da se formira novi aritmetički niz. navesti:
a. Nova razlika
b. Formula n-og pojma
c. Prvi broj n pojmova nove aritmetičke sekvence.
rasprava:
a.

b. Formula devetog pojma je
Un = a + (n-1) b
Un = 2 + (n-1) 2
Un = 2 + (2n-2)
Un = 2n
c. Broj prvog pojma n je
Sn= 1/2n (jedan + Un )
Sn= 1/2n (2 + 2n)
Sn= n (n + 1)
5. Pronađite prvi pojam, omjer i 8. pojam geometrijskog niza 2, 6, 18, 54, ...
rasprava:
a = 2
r = U2/ U1 = 6/2 = 3
zatim,
Un= arn-1
U8= ar8-1
U8= 2 (38-1)
U8= 2 (37)
U8= 2 (2.187)
U8= 4,374
6. Odredite broj geometrijskih serija 2 + 4 + 8 + 16 + ... (8 plemena)
rasprava:
jedan = 2
r = U2/ U1 = 4/2 = 2 (r> 1)
Broj redova do prvih 8 pojmova ima smisla n = 8

Dakle, prvih 8 pojmova geometrijskog niza je 510.
7. Redovi geometrije poznati su 1/8, 1/4, 1/2, 1, 2, 4, .... 2048. Odredite srednji pojam pravca.
rasprava:
a = 1/8
r = U2/ U1 = 1/8: 1/4 = 2
Un = 2.048
zatim,
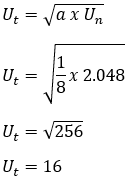
8. Poznato je da je geometrijski niz 1/32, 1/16, 1/8, 1/4, .... Između dva uzastopna izraza unose se tri broja na način da se formira novi geometrijski niz. navesti:
a. Pozitivan omjer novih geometrijskih linija
b. Formula devetog pojma nove geometrijske sekvence
c. Prvi broj n pojmova novog retka geometrije.
rasprava:
Geometrijski niz 1/32, 1/16, 1/8, 1/4, ... ili se također mogu poslužiti 2-5, 2 -4, 2-3, 2-2, ....
a. Razmotrimo dva uzastopna izraza, na primjer U1 i U2 = 1/32 i 1/16, tada:

b. Formula devetog pojma je
Un= arn-1
Un= 2-5(2n / 4-1)
Un= 2n / 4-6
c. Iznos n prvi termin je

9. Odredite beskonačni broj pojmova geometrijskog niza 1 + 1/2 + 1/4 + 1/8 + ...
rasprava:
a = 1
r = U2/ U1 = 1/2: 1 = 1/2
zatim,

10. Prvi pojam niza geometrija je 2, a zbroj do beskonačnosti je 4. Pronađite omjer.
rasprava:
a = 2
S∞ = 4
tada zamjenjujemo formulom S∞
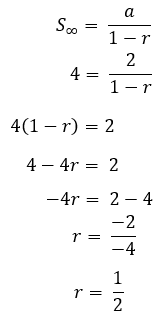
To je objašnjenje aritmetičkih i geometrijskih formula zajedno s primjerima pitanja i njihovom raspravom. Nadam se da je ovo korisno!








