נוסחאות חשבון וגיאומטריה עם דוגמאות לשאלות ודיונם
מאמר זה ידון בנוסחאות חשבון וגיאומטרי יחד עם דוגמאות לשאלות ודיונם.
אריתמטיקה וגיאומטריה הם הנושאים שלנוללמוד בבית הספר במתמטיקה. כאשר כאשר בחינות ארציות, בחינות כניסה לקולג 'או בחינות בהגשת מועמדות למשרות, לעתים קרובות יש שאלות על שתיהן.
לא רק זה, עלינו גם להיות מסוגלים להבחיןבין רצפים ושורות אריתמטיות או רצפים ושורות גיאומטריות, מכיוון שחוקי הרצפים והשורות יכולים להקל עלינו בהשלמת חישובים, כמו ריבית בנקאית, עליית ייצור ורווח / הפסד לעסק. בסדר, בואו נסתכל על ההסבר הבא!
נוסחאות אריתמטיות
-
שורה אריתמטית

התבונן בטבלה שלמעלה, התבונן כיצד ההבדל במספרים משמאל לימיננו? ואז, שים לב להבדל במספרים מלמעלה למטה?
מהתצפיות אנו מגלים שההבדל מקו אחד תמיד קבוע. לדוגמא משורה ימנית משמאלנו: 1, 2, 3, 4, 5 (ההבדל הוא 1).
5 - 1 = 4; 4 - 1 = 3; 3 - 1 = 2; 2 - 1 = 1
ומלמעלה למטה: 1, 6, 11, 16 (הפרש 5).
16 - 5 = 11; 11 - 5 = 6; 6 - 5 = 1
שורות כמו זה נקראות רצפי חשבון.
נקרא הפרש שיש לו ערך קבוע שונה ומסומל על ידי ב. באופן כללי ניתן לומר שאם Un הנוסחה ההברהn רצף אריתמטי, אז הוא חל
b = Un - Un-1
אם הקדנציה הראשונה (U.1) מסומל על ידי א וההבדל מסומל על ידי בואז הנוסחהn ניתן לגזור את הרצף כדלקמן.
U1= א
U2= U1 + b = א + ב
U3= U2 + b = (א + b) + b = a + 2b
U4= U3 + b = (א + 2b) + b = a + 3b
U5= U4 + b = (א + 3b) + b = a + 4b
אז, ניתן לנסח את התנאים לn מדרגות אריתמטיות הוא
Un= a + (n - 1)ב
תיאור:
Un= שבט לn
א = הברה ראשונה
b = שונה
n = שבטים רבים
-
סדרת חשבון
אם יתווספו מונחי הרצף האריתמטי, תתקבל סדרה אריתמטית. למשל U1, U2, U3, ……., Un הם אז שבטים בדרגות חשבון U1 + U2 + U3 + .... + Un קרא התקדמות חשבון. סדרות חשבון א n כתוב עם סימון ה- Sn עם Un= a + (n - 1)ב.
אז הנוסחה הכללית להתקדמות אריתמטית היא
ש.n= 1/2 n (a + Un)
ש.n= 1/2 n (2a + (n - 1) b)
תיאור:
ש.n= מספר התקדמויות חשבון
א = הברה ראשונה
b = שונה
Un= שבט לn
n = שבטים רבים
קבע את המונח לn רצף חשבון אם נוסחת המספרים ידועה n השבט הראשון. שבט לn ניתן לקבוע על ידי הנוסחה הבאה.
Un = Sn - ש.n-1
-
השבט האמצעי של קו אריאן או חשבון
אם אתה יודע את רצף החשבון הבא: U1, U2, U3, ……., Un, עם שבטים צועדים רביםזה מוזר, כך שיש מונח ממש באמצע הקו המחלק את הקו לשני חלקים שווים. נניח שהמונח האמצעי של הרצף הוא Ut. אז למצוא את המונח האמצעי הוא כדלקמן.

תיאור:
Ut= השבט האמצעי של דרגות חשבון
א = הברה ראשונה
Un= השבט האחרון של דרגות חשבון עם רבים n מוזר
-
הכנס בשורה אריתמטית
למשל U1, U2, U3, ……., Un, הוא רצף אריתמטי עם הברה ראשונית U1. אם בין שני מונחים רצופים מוכנסים k מספרים כך שנוצרים רצפי חשבון חדשים, רצפי האריתמטיקה החדשים נוצרים באופן הבא.
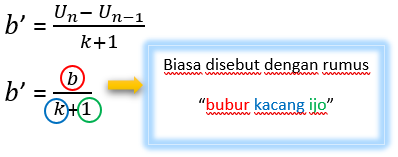
תיאור:
b '= הבדל חדש לאחר הכנסות
b = שונה לפני הכנסות
k = מספר מוכנס
נוסחאות גיאומטריה
-
קו הגיאומטריה
נסה להתבונן בשורות 1, 2, 4, 8, 16, .... ראה כי המונח הבא מתקבל על ידי הכפלת 2 במונח הקודם. רצף זה כולל את הרצף הגיאומטרי.
אז ניתן להסיק באופן כללי, רצף גיאומטרי הוא רצף של מספרים שכל שבט מתקבל מהמונח הקודם כפול מספר קבוע (קבוע). למספרים הקבועים האלה קוראים יחס (השוואה) ומסומל על ידי r.
אם U1, U2, U3, U4......., Un רצף גיאומטרי עם Un היא הנוסחה לn, ויחס r, ישים:
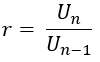
נוסחה כללית לשבטn רצף גיאומטרי עם המונח הראשון (U1) מוכרז א ויחס r, ניתן לגזור כדלקמן.
U1= א
U2= U1 x r = ar
U3= U2 x r = ar²
U4= U3 x r = ar3
::
Un= Un-1 x r = arn-2 x r = arn-1
כך השיג רצף גיאומטרי a, ar, ar², ...., arn-1.
אז הנוסחה הכללית שלn רצף גיאומטרי הוא
Un= arn-1
תיאור:
Un = שבט לn
א = הברה ראשונה
r = יחס
n = שבטים רבים
-
סדרת הגיאומטריה
אם U1, U2, U3, U4......., Un היא שורת גיאומטריה אז U1 + U2 + U3+ U4 + …… .. Un הוא א סדרת הגיאומטריה עם Un = arn-1.
נוסחה כללית לקביעת סכומים n ניתן לגזור את המונח הראשון ברצף הגיאומטרי כדלקמן.
למשל ש.n סימון סכומים n הברה ראשונה.
ש.n = U1 + U2 + U3 + …… .. Un
ש.n = א + ar + ar2 + ... + arn-1…………………………………………………………………(1)
אם כפול שני המקטעים r, אז
rSn = ar + ar2 + ar3 + ... + arn………………………………………………………………(2)
מההבדל במשוואות (1) ו- (2) אנו יכולים לקבל

אז הנוסחה של הסכום n המונח הראשון ברצף הגיאומטרי, שהוא כדלקמן.

תיאור:
ש.n = הסכום n הברה ראשונה
א = הברה ראשונה
r = יחס
n = שבטים רבים
-
השבט המרכזי של סדרת הקו או הגיאומטריה
לדוגמה, דע את הרצף הגיאומטרי הבא: U1, U2, U3, U4......., Un (מספר המונחים מוזר). המונח האמצעי של הקו הוא Ut, ואז הנוסחה היא כדלקמן.
תיאור:
Ut= רצף גיאומטרי אמצע אמצעי
א = הברה ראשונה
Un= הרצף הגיאומטרי האחרון עם המספר n מוזר
-
הכנס בשורה הגיאומטרית
אם בשורה הגיאומטרית מוכנס k מספרים בצורה כזו בין שני מונחים רצופים, כך שנוצרים קווים גיאומטריים חדשים. אז במציאת היחס החדש ניתן לנסח כדלקמן.

תיאור:
r '= יחס חדש לאחר הכניסה
r = יחס לפני הכניסה
k = מספר מוכנס

-
סדרת גיאומטריה ללא הגבלה
סדרת גאומטריה אינסופית היא סדרה גיאומטרית שלא ניתן לחתוך אותה על ידי רבים מהשבטים שלה. קחו למשל את הדוגמא הבאה!
א. 1 + 2 + 4 + 8 + ...
ב. 5 - 10 + 20 - 40 + ...
ג. 1 + 1/2 + 1/4 + 1/8 + ...
ד. 9 - 3 + 1 - 1/3 + ...
הסדרה שלמעלה היא דוגמא לסדרת גיאומטריה אינסופית. שקול את הדוגמאות a ו- b. הסדרה היא סדרות שונות כלומר סדרה שלא עוברת לערך מסוים ויש לה יחס r עם | r | > 1.
בשלב הבא, דוגמאות c ו- d הן סדרה מתכנסת, כלומר סדרה שהולכת לערך מסוים ויש לה יחס r עם | r | <1.
בסדרות מתכנסות, מספר המונחים לא יעלה על מחיר מסוים, אלא יתקרב למחיר מסוים. מחיר ספציפי זה נקרא מספר אינסופי של מונחים שמסומן על ידי S∞. ערך S∞ מייצג את ערך הגישה (גבול) של כל המונח (Sn) עם n אינסוף מתקרב. לכן ניתן לגזור את הנוסחה הסופית האינסופית מהסדרה הגיאומטרית עם המונח הראשון א, ו n → ∞.

מכיוון שהסדרה מתכנסת (| r | <1), עבור n → ∞, אז arn→ 0 כך ש

אז הנוסחה למספר הסדרות הגיאומטריות האינסופיות היא
שאלות ודיון לדוגמה
1. קבע את המונחים השישית והעשירית של השורות -3, 2, 7, 12, ...
דיון:
א = -3
ב = Un Un-1 = 2 - (-3) = 5
Un = a + (n-1) b, ואז:
U6 = (-3) + (6-1) 5 = 22
U10 = (-3) + (10-1) 5 = 42
2. מצא את 90 המונחים הראשונים בסדרת 2 + 4 + 6 + 8 +
דיון:
א = 2
ב = 4 - 2 = 2
n = 90
לאחר מכן,
ש.n= 1/2n (2א + (n-1)ב)
ש.n= 1/2 x 90 (2 (2) + (90-1) 2)
ש.n= 45 (4 + 178)
ש.n= 45 (182)
ש.n= 8,190
אז 90 התנאים הראשונים של הסדרה הם 8,190.
3. ידוע על רצף אריתמטי 3, 5, 7, 9, .... 1,007.
קבע את המונח האמצעי של הקו.
דיון:
א = 3
b = 5-7 = 2
Un = 1,007, אם כן:
Ut = 1/2 (א + Un)
Ut = 1/2 (3 + 1,007)
Ut = 1/2 (1,010)
Ut = 505
4. שורות ידועות 2, 12, 22, 32, ... בין שני מונחים רצופים מוכנסים 4 מספרים באופן שנוצר רצף אריתמטי חדש. לקבוע:
א. הבדל חדש
ב. הנוסחה של המונח התשיעי
ג. המספר הראשון n מונחים של הרצף האריתמטי החדש.
דיון:
א.

ב. הנוסחה המונחית התשיעית היא
Un = a + (n-1) ב
Un = 2 + (n-1) 2
Un = 2 + (2n-2)
Un = 2n
ג. המספר של המונח הראשון n הוא
ש.n= 1/2n (א + Un )
ש.n= 1/2n (2 + 2n)
ש.n= n (n + 1)
5. מצא את המונח הראשון, היחס והמונח השמיני בשורה הגיאומטרית 2, 6, 18, 54, ...
דיון:
א = 2
r = U2/ U1 = 6/2 = 3
לאחר מכן,
Un= arn-1
U8= ar8-1
U8= 2 (38-1)
U8= 2 (37)
U8= 2 (2,187)
U8= 4,374
6. קבע את מספר סדרות הגיאומטריה 2 + 4 + 8 + 16 + ... (8 שבטים)
דיון:
א = 2
r = U2/ U1 = 4/2 = 2 (r> 1)
פירושו של מספר השורות עד 8 המונחים הראשונים n = 8

אז, 8 המונחים הראשונים של הסדרה הגיאומטרית הם 510.
7. שורות גיאומטריה ידועות 1/8, 1/4, 1/2, 1, 2, 4, .... 2048. קבע את המונח האמצעי של הקו.
דיון:
א = 1/8
r = U2/ U1 = 1/8: 1/4 = 2
Un = 2,048
לאחר מכן,
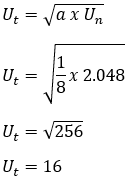
8. ידוע שהרצף הגיאומטרי הוא 1/32, 1/16, 1/8, 1/4, .... בין שני מונחים רצופים מוכנסים שלושה מספרים באופן שנוצר רצף גיאומטרי חדש. לקבוע:
א. יחס חיובי של קווי גיאומטריה חדשים
ב. הנוסחה המונחית התשיעית ברצף הגיאומטריה החדש
ג. המספר הראשון n מונחים בשורת הגיאומטריה החדשה.
דיון:
רצף גיאומטריה 1/32, 1/16, 1/8, 1/4, ... או שניתן להגיש גם 2-5, 2 -4, 2-3, 2-2, ....
א. שקול שתי מונחים רצופים, למשל U1 ואתה2 = 1/32 ו- 1/16, לאחר מכן:

ב. הנוסחה המונחית התשיעית היא
Un= arn-1
Un= 2-5(2n / 4-1)
Un= 2n / 4-6
ג. סה"כ n הקדנציה הראשונה היא

9. קבע את מספר המונחים האינסופי של הסדרה הגיאומטרית 1 + 1/2 + 1/4 + 1/8 + ...
דיון:
א = 1
r = U2/ U1 = 1/2: 1 = 1/2
לאחר מכן,

10. המונח הראשון בסדרת הגיאומטריה הוא 2 והסכום לאינסוף הוא 4. מצא את היחס.
דיון:
א = 2
ש.∞ = 4
ואז, אנו מחליפים את הנוסחה S∞
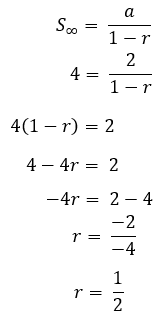
זה ההסבר לנוסחאות חשבון וגיאומטריה יחד עם דוגמאות לשאלות והדיון בהן. יכול להיות שימושי!








