אוסף נוסחאות טריגונומטריה עם דוגמאות לשאלות ודיונם

לאלו מכם שעדיין סטודנטיםומי שעבד כנראה למד מתמטיקה. נושא זה אכן נלמד לסטודנטים מאז בית הספר היסודי ועד סטודנטים באוניברסיטה.

אפילו מתמטיקה כלולה תמיד בבחינות בית הספר ובבחינות ארציות בכמה דרגות השכלה.

כי הנושא הזה גם מלא סטודנטיםשלעתים קרובות מתלונן כשהוא מקבל משימה לבצע בעיות במתמטיקה. אכן חלק מהנוסחאות במתמטיקה מספיקות בכדי לנקז את הנפש להבנה. נוסחה מתמטית אחת שקשה למדי ללמוד היא הנוסחה הטריגונומטרית.

תוכן עניינים

אוסף נוסחאות טריגונומטריה

דברו על נוסחאות טריגונומטריה ואז אתםילמדו על צורות משולש. מכיוון שנוסחת הטריגונומטריה היא נוסחה הבוחנת את הקשר בין זוויות לצדדים הקיימים בצורות משולש. ואילו הפונקציה הטריגונומטרית עצמה מחולקת לשלושה, כלומר הפונקציה של קונסינוס (cos), סינוס (sin), secan (sec), tangent (tan), cotangen (cotan), and cosecan (cosec).

1. נוסחת פונקציית טריגונומטריה

הנוסחה הטריגונומטרית הראשונה מגיעה מהפונקציות הטריגונומטריות שלמעלה. שם לכל נוסחה יש דרך לחשב מכל פינה במשולש. נוסחת הפונקציה הטריגונומטרית היא

עבור הנוסחה sin α משמש לחישוב צדדיםהחלק הקדמי מחולק על ידי הצד המשופע. בעוד הנוסחה cos α משמשת לחישוב הצד המחולק על ידי ההיפוטוזה. ושיזוף α הוא הנוסחה מהצד הקדמי של היפרנוזה במשולש. כדי להקל על זכירתם של שלוש פונקציות הנוסחה שלמעלה, תוכלו להשתמש בקיצורים הבאים.

SinDeMi

קיצור של סינוס קדמי משופע או נוסחת sin α.

CosSaMi

Lean Cosmetics או נוסחת cos α.

TanDeSa

והקיצור TanDeSa הוא הנוסחה הקדמית של המשיק או הנוסחה tan α.

2. נוסחאות זהות של טריגונומטריה

נוסחת הזהות הטריגונומטרית היא נוסחההשווה בין טריגונומטריה לבין משתני זווית x. כאשר משתנה ה- x מתקבל ממידה של מעלות ורדיאנים. ואילו הדרך לפתור את המשוואה sin x x = sin? ° (x? R) היא:

תחילה השתמשו ביחס הזווית sin (180º -? º) = sin? º וחטא (? º + k.360º) = sin? º. ואז נכנס למשוואה sin xº = sin? º להיות

אם חטא x⁰ = חטא?⁰ (x? r), אם כן:

x =? + k.360⁰ או x = (180⁰ ? ?) + k.360, עם k? ב

הערה: x נמצא במעלות

אם sin x = sin A (x? R), אז:

x = A + k.2? או x = (?? a) + k.2?, עם k? ב

הערה: x נמצא ברדיאנים

3. סכום והבדל של זווית טריגונומטריה

הנוסחה השלישית בטריגונומטריה היא הנוסחה לסכום ולהבדל בזוויות הטריגונומטריות. הנוסחה היא:

נוסחה זו משמשת להוספת זוויות ודפנות במשולש.

4. נוסחת כפל טריגונומטריה

באשר לכפל בזוויות ובצדי המשולש, אתה יכול להשתמש בנוסחת הכפל הטריגונומטרי שלמעלה.

5. נוסחאות טריגונומטריה ונוסחאות ההבדל

במשולש יש לא רק את נוסחת התוספת אלא יש גם צד שיש לתמצת בו זמנית מחפש את ההבדל עם הנוסחה לסכום ואת ההבדל הטריגונומטרי שלמעלה.

6. נוסחאות טריגונומטריה ו -3 זוויות

נוסחה טריגונומטרית כפולה וזוויתית ומשולשת

אם אתה מוצא בעיה בזוויות 2 ו -3 במשולש, השתמש בפורמולות 2 ו -3 בטריגונומטריה.

7. נוסחת חצי זווית של טריגונומטריה

הזוויות הניתנות לחישוב על משולש אינן רק זוויות מלאות אלא ניתן לחשב חצי זוויות של משולש בעזרת הנוסחה של חצי הזוויות הטריגונומטריות שלמעלה.

8. נוסחאות זווית מיוחדות של טריגונומטריה

בנוסף לשבע הנוסחאות שלמעלה, ישנן גם זוויות מיוחדות בנוסחת הטריגונומטריה

$0 ^ {o}$ , $30 ^ {o}$ , $45 ^ {o}$ , $60 ^ {o}$ , ו $90 ^ {o}$ . איפה לכל נוסחה זוויתית מיוחדתניתן לראות טריגונומטריה בתרשים למעלה. לגבי הנוסחה למציאת ערכים טריגונומטריים שקשורים בזווית המיוחדת שלמעלה, השתמש בנוסחה הבאה.

אז כשאתה עובד על בעיהtrigonometry אז אתה צריך לברר מראש אם הבעיה היא בעיה עם הנוסחה הרגילה של trigonometry או עם נוסחה מיוחדת של טריגונומטריה. מכיוון שכל נוסחה שתשתמש תתן תוצאות שונות כמו גם דיוק במענה על שאלות.

דוגמאות לטריגונומטריה

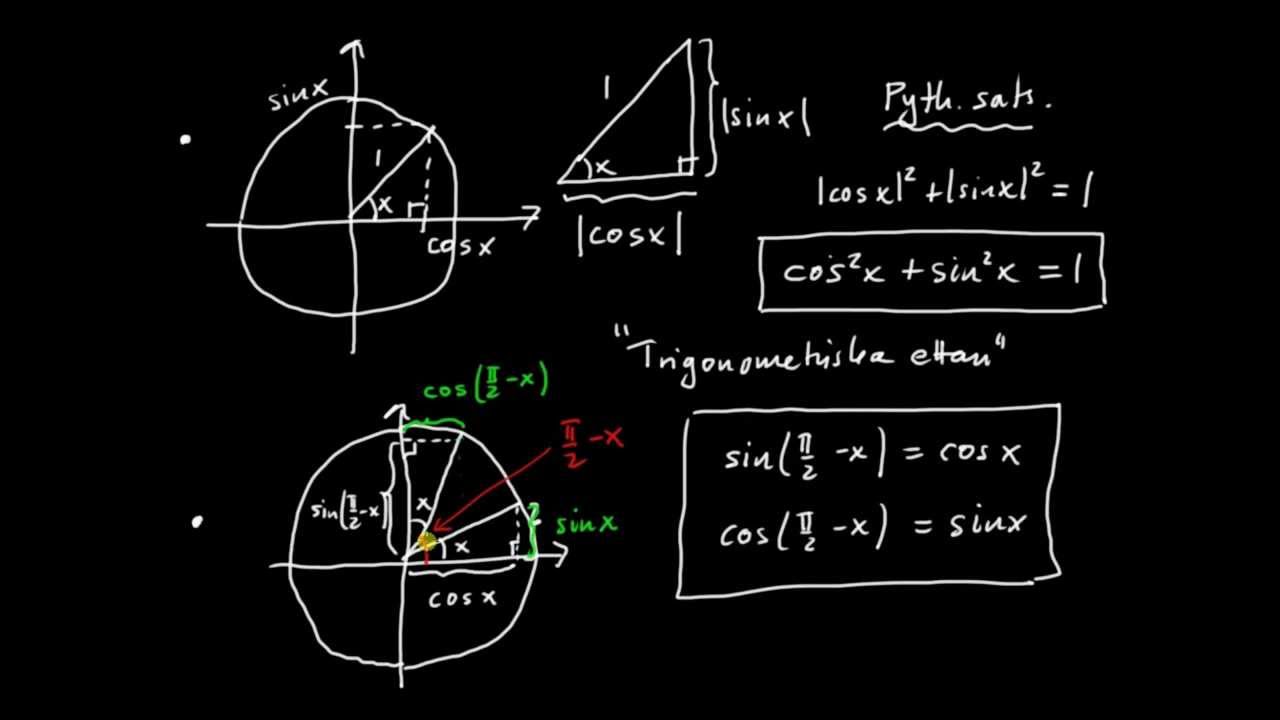
איך? האם אתה מבין בנוסחה הטריגונומטרית שלמעלה? אכן, הנוסחה די קשה להבנה, אך זה לא אומר שאתה לא יכול אם תמשיך לנסות. אתה יכול גם להבין נוסחאות טריגונומטריות באמצעות בעיות טריגונומטריות. באשר לכמה דוגמאות לשאלות על טריגונומטריה שתוכלו לנסות הן:

1. קבע את ערך החטא 105º + sin 15º

הבעיה הטריגונומטרית שלמעלה היא בעיית טריגונומטריה מסוג תוספת, כך שתוכלו להשתמש בנוסחה הטריגונומטרית של התוספת שהיא 2 sin ½ (A + B) cos ½ (A-B). התהליך הוא:

ערך החטא 105 ° + sin 15 ° = 2 sin ½ (105 + 15) ° cos ½ (105-15) °
= 2 sin ½ (102) ° cos ½ (90) °
= sin 60 ° cos 45 °

אז התשובה לבעיה sin 105º + sin 15º היא sin 60º cos 45º.

2. מצא את ערך המשוואה של sin xº sin 25º

יישוב השאלות לעיל, היינו:

x = 25⁰ + k.360⁰ או x = (180⁰ ? 25⁰) + k.360⁰

= 155⁰ + k.360⁰

אז, x = 25⁰ + k.360⁰ או 155 מעלות + k.360⁰

אז ערך המשוואה של sin xº sin 25º הוא x = 25⁰ + k.360⁰ או 155 מעלות + k.360^0.

3. קבע את ערך הכפל 2 cos 75º cos 15º

הבעיה השלישית היא מעל מודל הכפל הטריגונומטרי. הנוסחה המשמשת היא 2 cos A cos B = cos (A + B) + cos (A-B). הפיתרון לבעיה הוא:

2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75 - 15) °
= cos 90 ° + cos 60 °
= 0 + ½
= ½

אז התוצאה של הכפלת 2 cos 75º cos 15º היא ½.

4. א משולש ABC נקודה חדה, ידוע cos A = 4/5 וחטא B = 12/13, ואז חטא C הוא ...

מכיוון שלמשולש ABC יש זווית חדה, אז גם זוויות A, B ו- C חריפות, כך:

cos A = 4/5, ואז חטא A = 3/5,
חטא B = 12/13, ואז cos B = 5/13
A + B + C = 180 °, (מספר זוויות במשולש אחד = 180)
A + B = 180 - C
sin (A + B) = חטא (180 - C)
חטא א. cos B + cos A.sin B = sin C, (זוויות של משולשים קשורים זה בזה: sin (180-x) = sin x)
sin C = sin A.cos B + cos A.sin B
sin C = 3 / 5.5 / 13 + 4 / 5.12 / 13
חטא C = 15/65 + 48/65 = 63/65

מהנוסחה שלמעלה, ערך ה- C הוא 63/65

5. להחליט ערך החטא 120^o

לשאלה מספר 5 יש שתי דרכים לפתור אותה. הדרך הראשונה היא:

120 = 90 + 30

אז חטא 120^o ניתן לחשב בעזרת הנוסחה Sin 120^o = חטא (90^o + 30^o) = Cos 30^o (השיג ערך חיובי מכיוון ש- 120 מעלות ברבע II (2), כך שהתוצאה גם חיובית)
Cos 30^o = ½ √3

או בדרך השנייה, כלומר:

זהה ל- 180^o-80^º

חטא 120^o = חטא (180^o - 60^o) = חטא 60^o = ½ √3

אז התוצאה של חטא 120º היא ½ √3.

6. א למשולש ABC אורך צד AB = 6 ס"מ, BC = 8 ס"מ AC = 7 ס"מ. הערך של cos A הוא ..

איך לעשות את הבעיה למעלה עם הנוסחה:

Cos A = (AB² + AC²-BC²) / 2 (AB. AC)
Cos A = 6² + 7²-8² / 2 (6. 7)
Cos A = 36 + 49-64 / 2 (42)
Cos A = 21/84

כך שנמצא כי ה- A הוא 21/84.

7. הנקודות P ו- Q מבוטאות באמצעות קואורדינטות קוטביות. ואז קבעו את המרחק בין נקודות P ו- Q!

לבעיה שלמעלה, השתמש בנוסחה של consinus שהיא:

גודל זווית ה- POQ = 180^o - (75^o+45^o) = 60^o.
PQ² = OQ² + OP² - 2.OQ.OP cos ∠POQ
PQ² = 3² + 5² - 2.3.5 cos 60^o ג
PQ² = 9 + 25 - 30. 0.5
PQ² = 9 + 25 -15
PQ² = 19
PQ = √19 = 4.36