Hooke 's Law 공부 : 공식, 소리, 질문의 예 및 토론

훅의 법칙 소리

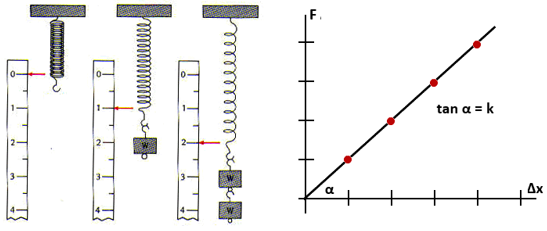
신축성이있는 훅 법칙은 동일합니다관련. 기본적으로 후크의 법칙은 물체의 탄성을 논의하는 법이기 때문입니다. 기억해야 할 것은 모든 탄성 물체가 고무로 만들어지는 것은 아닙니다. 특정 특성을 충족하는 모든 물체를 이미 탄성 물체라고 부를 수 있기 때문입니다. 훅 법칙의 소리는 다음과 같습니다.

"스프링에 가해지는 인장력이 재료의 탄성 한계를 초과하지 않으면, 스프링 길이의 증가는 인장력에 정비례하거나 비례합니다."

이름에서 알 수 있듯이, 고리 법은Robert Hooke라는 사람. Hooke가 탄성 물체, 스프링 및 기타 물체에 작용하는 힘을 연구하여 물체가 원래 크기로 돌아갈 수 있고 탄성 한계를 초과하지 않는 경우. 따라서 훅 법칙이 탄성 특성을 가진 물체에 적용 할 수있는 최대 힘을 논의하는 법이라면 결론을 내릴 수 있습니다.

실험으로 자주 사용되는 두 가지 개체탄성 법과 훅법은 껌과 고무 밴드입니다. 고무줄을 잡아 당기면 원래 모양으로 돌아갈 수 있습니다. 잇몸을 길게 늘리면 원래 모양으로 돌아올 수 없습니다. 고무가 탄성이고 껌이 플라스틱이기 때문입니다.

또한 읽어보십시오 : 파스칼의 법칙

훅의 법칙

고무 밴드와 잇몸 실험에서위의 훅 법은 고무 밴드에서만 작동합니다. 훅 법칙은 물체의 탄성 한계에 도달 할 때까지만 적용되기 때문입니다. 탄력적이지 않기 때문에 일찍 철회 된 잇몸은 그 고리 법칙에 영향을 미치지 않습니다. 쇠사슬 법의 공식은 다음과 같습니다.

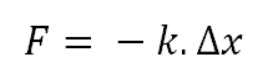
어디에 :

F = 힘 (N)
K = 스프링 상수 (N / m)
Δx = 스프링 길이 증가 (m)

스프링 전위 에너지는 다음과 같이 공식화됩니다. ep = ½ k Δx2

어디에 :

Ep = 스프링 전위 에너지 (J)
K = 스프링 상수 (N / m)
Δx = 스프링 길이 증가 (m)

설명은 다음과 같습니다.

스프링 시리즈 회로

2 개 이상의 스프링이 직렬로 배열 된 경우 스프링의 상수 값은 다음 방정식을 사용하여 계산할 수 있습니다. 1 / kp = 1 / k1 + 1 / k2 +. . .

병렬 스프링 회로

2 개 이상의 스프링이 병렬로 배열 된 경우 스프링의 상수 값은 다음 방정식을 사용하여 계산할 수 있습니다. kp = k1 + k2 +. . .

봄 잠재력 에너지

잠재적 에너지가 의미하는 것은스프링은 스프링의 탄성으로 인해 스프링에 저장된 에너지입니다. 그리고 잠재적 인 스프링 에너지의 양은 스프링을 늘리고 압축하기 위해 스프링에 가해지는 외력의 양에 달려 있습니다.

또한 읽기 옴의 법칙

Hooke의 법칙의 적용

hooke의 법칙은 검사하는 법이기 때문에물체의 탄력성에 관해이 고리 법에 기초하여 만들어지는 많은 것들이 있습니다. 일상 생활에서 쇠사슬 법의 적용은 다음과 같습니다.

1. 스프링 특성을 가진 스윙

도구 인 베이비 스윙을 본 적이 있습니까스프링으로 만든 스윙 어? 스프링은 스프링 특성을 가지므로 스프링 스윙을 당기거나 다른 방향으로 돌리면 원래 모양으로 돌아갑니다. 스프링 스윙의 훅크 법이 부패하기 어려운 탄성 때문에 매우 강하다고 말할 수 있습니다.

2. 현미경

현미경은 세기 말에 처음 발견되었습니다.16 일. 그러나 Robert Hooke가이 계측기에 고리 법칙을 적용한 후 17 세기 중반에보다 정교한 현미경이 개발되었습니다. 이전에는 현미경으로 만 큰 물체 만 볼 수있었습니다.

따라서 현미경에 적용된 고리 법칙이 존재하기 때문에 렌즈의 탄성이 증가합니다. 현미경을 사용하면 매우 작은 물체를 볼 수 있습니다.

3. 지구의 중력 속도를 측정하는 도구

속도 측정을위한 다양한 도구지구의 중력은 훅 법칙을 적용한 결과입니다. 일반적으로 이러한 도구는 지구의 석유 및 가스, 광물, 지각 화산, 지열 등을 탐험하는 데 사용됩니다.

4. 차량 기어 컴파일러

모든 좋은 동력 차량두 바퀴와 네 바퀴 모두 기어가 있습니다. 스틱이 자동차 기어에 배치되는 곳은 운송 분야의 일상 생활에서 구제법을 적용하는 것입니다.

또한 읽어보십시오 : 키르 히프의 법칙 I과 II

5. 망원경

생물체를보기 위해 현미경을 사용한다면매우 작은 크기의 현미경 또는 생물. 따라서 망원경은 우주에서 물체를 보는 데 사용됩니다. 고리 법칙을 채택하면 이제이 망원경을 사용하여 하늘에서 태양계의 배열을 볼 수 있습니다.

6. 크로노 미터 / 시간 거즈

크로노 미터를 알고 있습니까? 크로노 미터 또는 스크린 워치라고도하는 것은 광대 한 바다에있을 때 선박의 위치 나 선을 결정하는 데 사용되는 장치입니다. 이 크로노 미터의 제작도 훅 법칙의 소리에 기초합니다.

7. 시간당

훅법의 다음 적용은 제품에 있습니다시간을 표시하기 위해 여전히 사용하는 시간. 어쩌면 이번과 같은 시간 모델은 찾기가 매우 어려울 수 있지만 과거에는 가장 인기있는 시계 모델 중 하나가되었습니다.

Hooke의 법적 질문의 예

생활에 구부러진 법의 일부 적용기본적으로 훅법이 모든 사람의 삶에 매우 유익하다면 위의 일일 결론은 분명히 도출 될 수 있습니다. 특히이 법이 Robert Hooke라는 유명한 과학자에 의해 만들어진 경우. 그리고 쇠사슬 법을 만드는 과정에서 오늘날 과학자들에게 큰 혜택을주기 위해 자의적인 것은 아닙니다.

쇠사슬 법을 더 잘 이해하려면 아래 예제 질문으로 연습 해 봅시다!

1. 힘을 가한 후 스프링의 길이는 0.25 미터 증가합니다. 스프링이 400 N / m을 읽는다면. 이번 봄에는 어떤 힘이 있습니까?

알려진 :
x = 0.25m
k = 400 N / m

F에게 물었다 ...?

답변

F = k. x
F = 400 N / m x 0.25m
F = 100 N

스프링에 가해지는 힘은 100 뉴턴입니다.

2. 50 N의 힘이 주어지면 상수 200 N / m의 스프링. 스프링 길이의 증가를 결정하십시오!

정산 :

Hooke의 법칙에 따른 스프링의 길이는

Δx = Fk = 50200 = 0.25m

그런 다음 스프링 길이 증가 값은 0.25m입니다.