Aritmetikos ir geometrijos formulės su klausimų pavyzdžiais ir jų aptarimas
Šiame straipsnyje bus aptariamos aritmetinės ir geometrinės formulės, pateikiami klausimų pavyzdžiai ir jų aptarimas.
Aritmetika ir geometrija yra mūsų temosmokytis mokykloje matematikos. Kai vyksta valstybiniai egzaminai, stojamieji egzaminai ar egzaminai, kai kreipiamasi dėl darbo, dažnai kyla klausimų apie abu.
Ne tik tai, mes taip pat turime mokėti atskirtitarp aritmetinių sekų ir eilučių arba geometrinių sekų ir eilučių, nes sekų ir eilučių taisyklės gali mums padėti atlikti skaičiavimus, tokius kaip banko palūkanos, gamybos padidėjimas ir verslo pelnas / nuostoliai. Gerai, pažiūrėkime į šį paaiškinimą!
Aritmetinės formulės
-
Aritmetinė eilutė

Pažvelkite į aukščiau pateiktą lentelę, stebėkite, kaip skiriasi skaičius iš kairės į dešinę? Ir tada stebėkite skaičių skirtumą nuo viršaus iki apačios?
Iš stebėjimų pastebime, kad skirtumas tarp vienos eilutės visada yra fiksuotas. Pavyzdžiui, iš dešinės eilės į kairę: 1, 2, 3, 4, 5 (skirtumas yra 1).
5 - 1 = 4; 4 - 1 = 3; 3 - 1 = 2; 2 - 1 = 1
Ir iš viršaus į apačią: 1, 6, 11, 16 (skirtumas 5).
16 - 5 = 11; 11 - 5 = 6; 6 - 5 = 1
Tokios eilutės vadinamos aritmetinėmis sekomis.
Skirtumas, turintis fiksuotą vertę, vadinamas skirtingi ir yra simbolizuojamas b. Apskritai galima sakyti, kad jei Un yra skiemens formulėn aritmetinė seka, tada ji taikoma
b = Un - Un-1
Jei pirmoji kadencija (U.1) simbolizuojamas a o skirtumą simbolizuoja b, tada termino formulėn seka gali būti išvedama taip.
U1= a
U2= U1 + b = a + b
U3= U2 + b = (a + b) + b = a + 2b
U4= U3 + b = (a + 2b) + b = a + 3b
U5= U4 + b = (a + 3b) + b = a + 4b
Taigi, terminai gali būti suformuluotin aritmetinių gretų yra
Un= a + (n - 1)b
Aprašymas:
Un= gentis įn
a = pirmasis skiemuo
b = skirtingi
n = daugybė genčių
-
Aritmetikos serija
Jei sudėti aritmetiniai sekos terminai, gaunama aritmetinė seka. Pavyzdžiui U1, U2, U3, ……., Un yra aritmetinių gretų gentys, tada U1 + U2 + U3 + .... + Un paskambino aritmetinė progresija. Aritmetinė serija iš n parašyta su S notacijan su Un= a + (n - 1)b.
Taigi, bendra aritmetinio progresijos formulė yra
S.n= 1/2 n (a + Un)
S.n= 1/2 n (2a + (n - 1) b)
Aprašymas:
S.n= aritmetinių progresijų skaičius
a = pirmasis skiemuo
b = skirtingi
Un= gentis įn
n = daugybė genčių
Nustatykite terminą ikin aritmetinė seka, jei skaičiaus formulė yra žinoma n pirmoji gentis. Gentis įn gali būti nustatomas pagal šią formulę.
Un = Sn - S.n-1
-
Vidurinė Arisano linijos arba aritmetikos gentis
Jei žinote šią aritmetinę seką: U1, U2, U3, ……., Un, su daugybe aritmetinių žygiuojančių genčiųyra nelyginis, taigi tiesiai viduryje yra terminas, padalijantis liniją į 2 lygias dalis. Tarkime, kad vidutinis sekos terminas yra Ut. Taigi rasti tarpinį terminą yra taip.

Aprašymas:
Ut= vidurinė aritmetikos rango gentis
a = pirmasis skiemuo
Un= paskutiniosios aritmetikos genties rangų su daugeliu n keista
-
Įdėkite į aritmetinę eilutę
Pavyzdžiui U1, U2, U3, ……., Un, yra aritmetinė seka su pradiniu skiemeniu U1. Jei įterpiami du terminai iš eilės k skaičiai tokie, kad susidaro naujos aritmetinės sekos, skirtingos naujos aritmetinės sekos formuojamos taip.
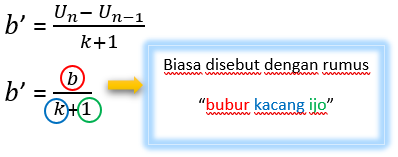
Aprašymas:
b ’= naujas skirtumas po intarpų
b = skiriasi prieš įterpimą
k = įterptas skaičius
Geometrijos formulės
-
Geometrijos linija
Pabandykite laikytis 1, 2, 4, 8, 16 eilutės. Žiūrėkite, kad kitas terminas būtų gaunamas padauginus iš ankstesniojo 2. Ši seka apima geometrinę seką.
Taigi, galima daryti išvadą apskritai, geometrinė seka yra kiekvienos genties skaičių seka, gauta iš ankstesnio termino, padauginta iš pastovaus skaičiaus (konstanta). Šie fiksuoti numeriai yra vadinami santykis (palyginimas) ir simbolizuoja r.
Jei U1, U2, U3, U4......., Un geometrinė seka su Un yra formulėn, ir santykis r, taikoma:
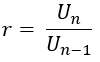
Bendra genties formulėn geometrinė seka su pirmąja kadencija (U1) yra deklaruojama a ir santykis r, gali būti išvedama taip.
U1= a
U2= U1 x r = ar
U3= U2 x r = ar²
U4= U3 x r = ar3
::
Un= Un-1 x r = arn-2 x r = arn-1
Tokiu būdu gauta geometrinė seka a, ar, ar², ...., arn-1.
Taigi, bendra formulėn geometrinė seka yra
Un= arn-1
Aprašymas:
Un = gentis įn
a = pirmasis skiemuo
r = santykis
n = daugybė genčių
-
Geometrijos serija
Jei U1, U2, U3, U4......., Un yra geometrijos eilutė tada U1 + U2 + U3+ U4 + …… .. Un yra a geometrijos serija su Un = arn-1.
Bendra sumų nustatymo formulė n pirmasis geometrinės sekos terminas gali būti išvestas taip.
Pavyzdžiui S.n sumų žymėjimas n pirmasis skiemuo.
S.n = U1 + U2 + U3 + …… .. Un
S.n = a + ar + ar2 + ... .. + arn-1…………………………………………………………………(1)
Jei abu segmentai padauginami r, tada
rSn = ar + ar2 + ar3 + ... .. + arn………………………………………………………………(2)
Iš lygčių (1) ir (2) skirtumų galime gauti

Taigi, sumos formulė n pirmasis geometrinės sekos terminas, kuris yra toks.

Aprašymas:
S.n = suma n pirmasis skiemuo
a = pirmasis skiemuo
r = santykis
n = daugybė genčių
-
Centrinė linijos arba geometrijos serijos gentis
Pvz., Žinokite šią geometrijos eilutę: U1, U2, U3, U4......., Un (žodžių skaičius nelyginis). Vidurinis linijos terminas yra Ut, tada formulė yra tokia.
Aprašymas:
Ut= vidutinės trukmės geometrinė seka
a = pirmasis skiemuo
Un= paskutinio termino geometrinė seka su skaičiumi n keista
-
Įterpti į geometrijos eilutę
Jei į geometrijos eilutę įterpiama k skaičiai tokiu būdu tarp dviejų iš eilės einančių žodžių, kad susidarytų naujos geometrinės linijos. Taigi ieškant naujo santykio galima suformuluoti taip.

Aprašymas:
r ’= naujas santykis po įdėjimo
r = santykis prieš įterpimą
k = įterptas skaičius

-
Neribota geometrijos serija
Begalinė geometrijos seka yra geometrinė seka, kurios negali suskaidyti daugelis jos genčių. Apsvarstykite šį pavyzdį!
a. 1 + 2 + 4 + 8 + ...
b. 5–10 + 20–40 + ...
c. 1 + 1/2 + 1/4 + 1/8 + ...
d. 9 - 3 + 1 - 1/3 + ...
Aukščiau pateiktos serijos yra begalinės geometrijos sekos pavyzdys. Apsvarstykite a ir b pavyzdžius. Serija yra skirtingos serijos, y., serija, kuri neatitinka tam tikros vertės ir turi santykį r su | r | > 1.
Toliau pateikiami c ir d pavyzdžiai konvergencijos serijos, y., serija, einanti į tam tikrą vertę ir turinti santykį r su | r | <1.
Susiliejančiose serijose terminų skaičius neviršys tam tikros kainos, bet artės prie tam tikros kainos. Ši konkreti kaina vadinama begalinis terminų skaičius kurį žymi S∞. S reikšmė∞ žymi viso termino artėjimo vertę (ribą) (Sn) su n artėjant prie begalybės. Todėl begalinės serijos formulę galima išvesti iš geometrinės eilutės su pirmuoju terminu a, ir n → ∞.

Nes serija suartėja (| r | <1), skirtas n → ∞, tada arn→ 0 kad taip

Taigi begalinių geometrinių eilučių skaičiaus formulė yra
Klausimų ir diskusijų pavyzdys
1. Nustatykite 6-ą ir 10-ą eilučių -3, 2, 7, 12, ... terminus.
Diskusija:
a = -3
b = Un Un-1 = 2 - (-3) = 5
Un = a + (n-1) b, tada:
U6 = (-3) + (6-1) 5 = 22
U10 = (-3) + (10-1) 5 = 42
2. Suraskite pirmuosius 90 2 + 4 + 6 + 8 + serijų terminų
Diskusija:
a = 2
b = 4 - 2 = 2
n = 90
tada,
S.n= 1/2n (2a + (n-1)b)
S.n= 1/2 x 90 (2 (2) + (90-1) 2)
S.n= 45 (4 + 178)
S.n= 45 (182)
S.n= 8,190
Taigi, pirmieji 90 serijos terminų yra 8 190.
3. Yra žinoma 3, 5, 7, 9, .... aritmetinė seka.
Nustatykite tiesės vidurį.
Diskusija:
a = 3
b = 5–7 = 2
Un = 1,007, tada:
Ut = 1/2 (a + Un)
Ut = 1/2 (3 + 1 007)
Ut = 1/2 (1 010)
Ut = 505
4. Žinomos 2, 12, 22, 32 eilutės ... Tarp dviejų iš eilės einančių 4 skaičių įterpiama taip, kad susidarytų nauja aritmetinė seka. Nustatyti:
a. Naujas skirtumas
b. N-osios formulės formulė
c. Naujosios aritmetinės sekos pirmieji skaičiai n.
Diskusija:
a.

b. Devintojo termino formulė yra
Un = a + (n-1) b
Un = 2 + (n-1) 2
Un = 2 + (2n – 2)
Un = 2n
c. Pirmosios kadencijos skaičius n yra
S.n= 1/2n (a + Un )
S.n= 1/2n (2 + 2n)
S.n= n (n + 1)
5. Raskite geometrinės sekos 2, 6, 18, 54, pirmąjį terminą, santykį ir 8-ąjį terminą ...
Diskusija:
a = 2
r = U2/ U1 = 6/2 = 3
tada,
Un= arn-1
U8= ar8-1
U8= 2 (38-1)
U8= 2 (37)
U8= 2 (2 187)
U8= 4 374
6. Nustatykite 2 + 4 + 8 + 16 + geometrijos eilių skaičių ... (8 gentys)
Diskusija:
a = 2
r = U2/ U1 = 4/2 = 2 (r> 1)
Eilučių skaičius iki pirmųjų 8 kadencijų reiškia n = 8

Taigi, pirmieji 8 geometrinės eilutės terminai yra 510.
7. Geometrijos eilutės žinomos 1/8, 1/4, 1/2, 1, 2, 4, .... 2048. Nustatykite tiesės vidurį.
Diskusija:
a = 1/8
r = U2/ U1 = 1/8: 1/4 = 2
Un = 2 048
tada,
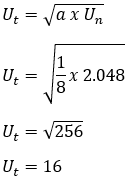
8. Yra žinoma, kad geometrinė seka yra 1/32, 1/16, 1/8, 1/4, .... Tarp dviejų iš eilės esančių žodžių trys skaičiai įterpiami taip, kad susidarytų nauja geometrinė seka. Nustatyti:
a. Teigiamas naujų geometrinių linijų santykis
b. N-oji naujos geometrijos sekos formulė
c. Pirmieji naujos geometrijos eilutės skaičiai n.
Diskusija:
Geometrijos seka 1/32, 1/16, 1/8, 1/4, ... arba taip pat gali būti patiekiami 2-5, 2 -4, 2-3, 2-2, ....
a. Apsvarstykite du terminus iš eilės, pavyzdžiui, U1 ir tu2 = 1/32 ir 1/16, tada:

b. Devintojo termino formulė yra
Un= arn-1
Un= 2-5(2n / 4-1)
Un= 2n / 4-6
c. viso n pirmoji kadencija yra

9. Nustatykite begalinį skaičių geometrinių sekų 1 + 1/2 + 1/4 + 1/8 + ...
Diskusija:
a = 1
r = U2/ U1 = 1/2: 1 = 1/2
tada,

10. Pirmasis geometrijos eilutės terminas yra 2, o suma iki begalybės - 4. Raskite santykį.
Diskusija:
a = 2
S.∞ = 4
tada mes pakeičiame formulę S∞
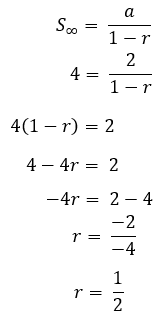
Tai yra aritmetinių ir geometrinių formulių paaiškinimas, klausimų pavyzdžiai ir jų aptarimas. Gali būti naudinga!








