Trigonometrijos formulių rinkinys su klausimų pavyzdžiais ir jų aptarimas

Tiems iš jūsų, kurie vis dar esate studentaio dirbę asmenys privalo būti studijavę matematiką. Šis dalykas iš tikrųjų buvo mokomas studentams nuo pagrindinės mokyklos iki universiteto studentų.

Net matematika visuomet įtraukiama į mokyklinius egzaminus ir valstybinius egzaminus keliuose švietimo lygmenyse.

Nes šis dalykas taip pat yra pilnas studentųkuris dažnai skundžiasi gavęs užduotį atlikti matematikos problemas. Iš tikrųjų kai kurių matematikos formulių pakanka, kad suprastų protas. Viena matematinė formulė, kurią gana sunku išmokti, yra trigonometrinė formulė.

Turinys

Trigonometrijos formulių kolekcija

Tuomet kalbėk apie trigonometrijos formulessužinos apie trikampio formas. Nes trigonometrijos formulė yra formulė, tirianti trikampio formos kampų ir kraštinių santykį. Nors pati trigonometrinė funkcija yra padalinta į tris, ty konsuso (cos), sinuso (sin), secan (sek), liestinės (tan), cotangen (cotan) ir cosecan (cosec) funkciją.

1. Trigonometrijos funkcijos formulė

Pirmoji trigonometrinė formulė gaunama iš aukščiau pateiktų trigonometrinių funkcijų. Kur kiekviena formulė turi būdą, kaip apskaičiuoti iš kiekvieno trikampio kampo. Trigonometrinės funkcijos formulė yra

Formulės skaičiavimui naudojama sin αpriekis padalintas nuožulniai. Kol formulė cos α naudojama apskaičiuojant pusę, padalintą iš hipotenuzės. Ir tan α yra trikampio hipotenuzės iš priekinės pusės formulė. Kad būtų lengviau atsiminti tris aukščiau pateiktas formulės funkcijas, galite naudoti šias santrumpas.

„SinDeMi“

Priekinio sinuso arba sin α formulės santrumpa.

„CosSaMi“

Liesos kosmetikos arba cos α formulė.

„TanDeSa“

O santrumpa „TanDeSa“ reiškia „Side Front Tangent“ arba „tan α“ formulę.

2. Trigonometrinės tapatybės formulės

Trigonometrinė tapatybės formulė yra formulėpalyginkite trigonometriją su x kampo kintamaisiais. Kur x kintamasis gaunamas iš laipsnių ir radianų dydžio. Kadangi lygties sin xº = sin? ° (x? R) lygtis gali būti išspręsta taip:

Pirmiausia naudokite kampo santykį sin (180º -? º) = sin º º ir sin (º º + k.360 º) = sin º º. Tada įveskite lygtį sin xº = sin? º be

Jei nuodėmė x⁰ = nuodėmė?⁰ (x? R), tada:

x =? + k.360⁰ arba x = (180⁰ ? ?) + k.360, su k? B

Pastaba: x yra laipsniais

Jei sin x = sin A (x? R), tada:

x = A + k.2? arba x = (?? a) + k.2?, su k? B

Pastaba: x yra radianuose

3. Trigonometrijos kampo dydis ir skirtumas

Trečioji trigonometrijos formulė yra trigonometrinių kampų sumos ir skirtumų formulė. Formulė yra:

Ši formulė naudojama sudėti kampus ir kraštines trikampyje.

4. Trigonometrijos daugybos formulė

Kalbant apie daugybę trikampio kampų ir šonų, galite naudoti aukščiau pateiktą trigonometrinę daugybos formulę.

5. Trigonometrijos dydis ir skirtumų formulės

trigonometrijos-skaičiaus ir skirtumo formulė

Trikampyje yra ne tik sudėjimo formulė, bet yra ir pusė, kuri turi būti sumuojama tuo pačiu metu ieškant skirtumo su sumos formule ir trigonometriniu skirtumu aukščiau.

6. Trigonometrijos dvigubos ir 3 kampų formulės

trigonometrinė dvigubo kampo ir trigubo formulė

Jei pastebėsite trikampio 2 ir 3 kampų problemą, naudokite trigonometrijos formules 2 ir 3.

7. Trigonometrijos pus kampo formulė

Kampai, kuriuos galima apskaičiuoti trikampyje, yra ne tik pilni kampai, bet ir trikampio pus kampai gali būti apskaičiuojami pagal aukščiau pateiktą trigonometrinių pus kampų formulę.

8. Trigonometrijos specialiosios kampo formulės

Be aukščiau pateiktų septynių formulių, trigonometrijos formulėje yra ir specialūs kampai

$0 ^ {o}$ , $30 ^ {o}$ , $45 ^ {o}$ , $60 ^ {o}$ ir $90 ^ {o}$ . Kur kiekvienai specialiai kampinei formuleiAukščiau esančioje diagramoje galite pamatyti trigonometriją. Kalbant apie formulę, kaip surasti trigonometrines reikšmes, kurios turi ką nors bendro su aukščiau pateiktu specialiu kampu, naudokite šią formulę.

Taigi, kai jūs dirbate su problematrigonometrija, tada jūs turite iš anksto išsiaiškinti, ar problema yra įprastos trigonometrijos formulės, ar specialios trigonometrinės problemos formulės problema. Nes kiekviena naudojama formulė duos skirtingus rezultatus ir tikslumą atsakant į klausimus.

Trigonometrijos pavyzdžiai

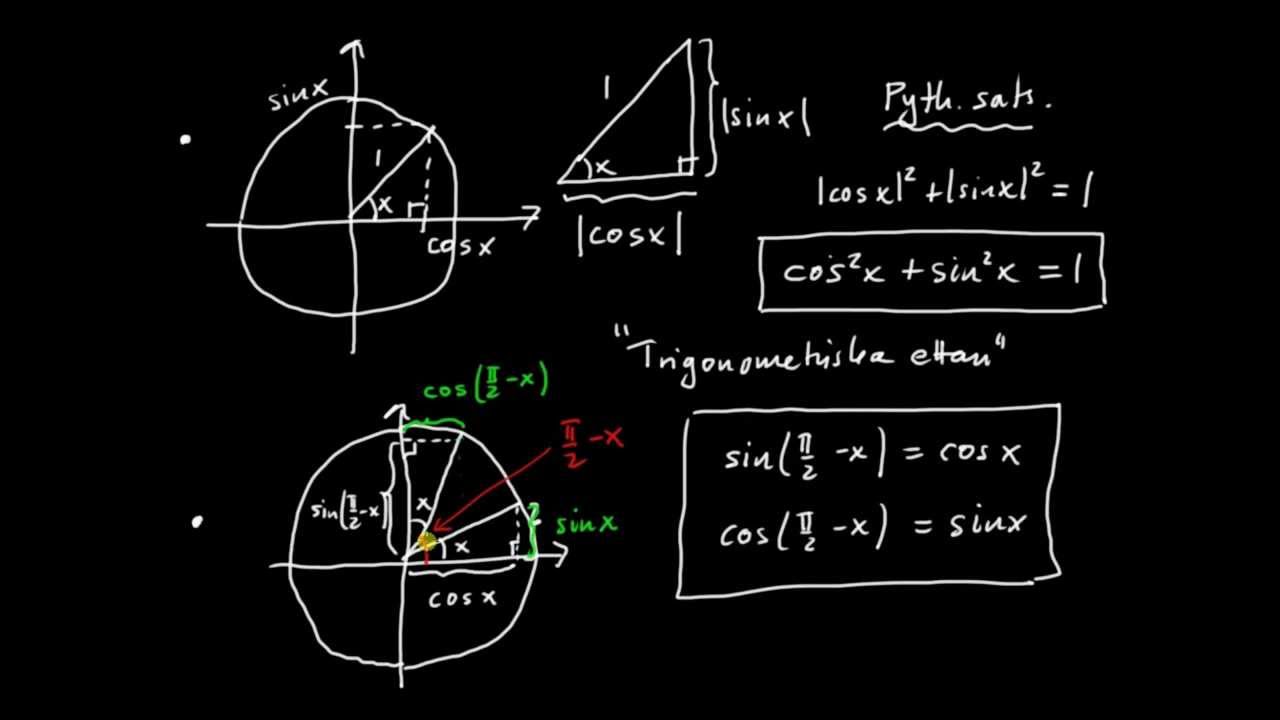
Trigonometrijos formulės ir pavyzdžių problemos

Kaip? Ar jūs suprantate apie aukščiau pateiktą trigonometrinę formulę? Iš tikrųjų formulę gana sunku suprasti, tačiau tai nereiškia, kad negalite, jei ir toliau bandote. Taip pat galite suprasti trigonometrines formules per trigonometrines problemas. Kai kurie klausimų apie trigonometriją pavyzdžiai, kuriuos galite išbandyti, yra šie:

1. Nustatykite nuodėmės vertę 105º + sin 15º

Aukščiau pateikta trigonometrinė problema yra papildomo tipo trigonometrijos problema, todėl galite naudoti papildomą trigonometrinę formulę, kuri yra 2 sin ½ (A + B) cos ½ (A-B). Procesas yra toks:

sin reikšmė 105 ° + sin 15 ° = 2 sin ½ (105 + 15) ° cos ½ (105-15) °
= 2 sin ½ (102) ° cos ½ (90) °
= sin 60 ° cos 45 °

Taigi atsakymas į problemą sin 105º + sin 15º yra sin 60º cos 45º.

2. Nustatykite lygties reikšmę: sin xº sin 25º

Aukščiau pateiktų klausimų sprendimas, būtent:

x = 25⁰ + k.360⁰ arba x = (180⁰ ? 25⁰) + k.360⁰

= 155⁰ + k.360⁰

Taigi, x = 25⁰ + k.360⁰ arba 155º + k.360⁰

Taigi lygties reikšmė sin xº sin 25º yra x = 25⁰ + k.360⁰ arba 155º + k.360^0.

3. Nustatykite dauginimo reikšmę 2 cos 75º cos 15º

Trečioji problema yra aukščiau trigonometrinio daugybos modelio. Naudojama formulė yra 2 cos A cos B = cos (A + B) + cos (A-B). Problemos sprendimas:

2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75 - 15) °
= cos 90 ° + cos 60 °
= 0 + ½
= ½

Taigi, padauginus iš 2 cos 75º cos 15º, rezultatas yra ½.

4. a trikampio ABC aštrus taškas, žinomas cos A = 4/5 ir sin B = 12/13, tada sin C yra ...

Kadangi trikampis ABC turi aštrų kampą, tada kampai A, B ir C taip pat yra aštrūs, taigi:

cos A = 4/5, tada sin A = 3/5,
sin B = 12/13, tada cos B = 5/13
A + B + C = 180 °, (kampų skaičius viename trikampyje = 180)
A + B = 180 - C
sin (A + B) = sin (180 - C)
nuodėmė A. cos B + cos A.sin B = sin C, (tarpusavyje susijusių trikampių kampai: sin (180-x) = sin x)
sin C = sin A.cos B + cos A.sin B
sin C = 3 / 5,5 / 13 + 4 / 5,12 / 13
sin C = 15/65 + 48/65 = 63/65

Pagal aukščiau pateiktą formulę sin C vertė yra 63/65

5. Nuspręskite nuodėmės vertė 120^o

5 klausimui spręsti yra du būdai. Pirmasis būdas yra:

120 = 90 + 30

Taigi nuodėmė 120^o galima apskaičiuoti naudojant formulę Sin 120^o = Nuodėmė (90^o + 30^o) = 30 Cos^o (gauta teigiama vertė, nes 120º yra II kvadrante (2), taigi rezultatas taip pat teigiamas)
Cos 30^o = ½ √3

Arba antruoju būdu, būtent:

Tas pats kaip 180^o-80^º

Nuodėmė 120^o = Nuodėmė (180^o - 60^o) = nuodėmė 60^o = ½ √3

Taigi nuodėmės 120º rezultatas yra ½ √3.

6. a ABC trikampio kraštinės ilgis AB = 6 cm, BC = 8 cm AC = 7 cm. Cos A reikšmė yra ..

Kaip išspręsti aukščiau pateiktą problemą, turite šią formulę:

„Cos A“ = (AB² + AC²-BC²) / 2 (AB. AC)
„Cos A“ = 6² + 7² – 8² / 2 (6. 7)
„Cos A“ = 36 + 49–64 / 2 (42)
COS A = 21/84

Taigi nustatyta, kad cos A yra 21/84.

7. Taškai P ir Q išreiškiami naudojant polines koordinates. Tada nustatykite atstumą tarp taškų P ir Q!

Norėdami išspręsti aukščiau pateiktą problemą, naudokite konsuso formulę, kuri yra:

POQ kampo dydis = 180^o - (75^o+45^o) = 60^o.
PQ² = OQ² + OP² - 2.OQ.OP cos ∠POQ
PQ² = 3² + 5² - 2.3.5 cos 60^o c
PQ² = 9 + 25 - 30. 0,5
PQ² = 9 + 25 -15
PQ² = 19
PQ = √19 = 4,36