Die Kreisformel und ihre Beispielfragen und Diskussion
Wir entkommen nicht den kreisförmigen Objekten, die uns umgeben. Wie beim Lernen in der Schule möchten Sie ein Kunstwerk oder andere Bedürfnisse machen.
Die Kenntnis der Kreisformeln hilft uns in unserem täglichen Leben. Einer von ihnen ist um den Kreis herum. Dieser Artikel wird über diskutieren die Formel um den Kreis mit Beispielen für Probleme und deren Diskussion. Hier ist die Erklärung!
Umfangsformel
Beachten Sie, dass der Umfang die Summe aller Umrisse in einer Ebene ist.

Es gibt zwei Formeln zum Umsehen eines Kreises:
1. Kreisen Sie den Kreis mit einem Durchmesser ein
Kreise mit einem bekannten Durchmesser können mit der Formel gefunden werden:

Beschreibung:
K = Um den Kreis herum
π = 22/7 oder 3,14
d = Kreisdurchmesser oder 2-facher Radius des Kreises
2. Kreisen Sie den Kreis mit den Fingern ein
Der Kreis, dessen Radius bekannt ist, kann mit folgender Formel durchsucht werden:

K = Um den Kreis herum
π = 22/7 oder 3,14
r = Kreisradius oder 1/2 des Kreisdurchmessers
Um die Berechnungen zu vereinfachen, werden die beiden Formeln mit Anmerkungen für den Wert π wie folgt verwendet:
- Wenn der Wert des Radius oder Durchmessers eines Kreises durch 7 geteilt werden kann, verwenden Sie den Wert π von 22/7.
-
Wenn der Wert des Radius oder Durchmessers eines Kreises nicht durch 7 geteilt werden kann, verwenden Sie den Wert π von 3,14.
Beispiele für Kreiskreise und ihre Diskussion
1. Der Radius des Kreises beträgt 49 cm. Berechnen Sie den Umfang des Kreises!
Diskussion:
r = 49 cm
Beantwortet:
K = 2πr
K = 2 · 22/7 · 49 cm
K = 308 cm
2. Der Durchmesser des Kreises beträgt 25 cm. Berechnen Sie den Umfang des Kreises!
Diskussion:
d = 25 cm
Beantwortet:
K = πd
K = 3,14 x 25 cm
K = 78,5 cm
3. Bekannt um den Kreis 28,26 cm. Was ist der Durchmesser des Kreises?
Diskussion:
K = 28,26 cm
Beantwortet:
K = πd
28,26 cm = 3,14 x d
d = 28,26: 3,14 cm
d = 9 cm
4. Beachten Sie das folgende Bild!

Eine kreisförmige Münze hat einen Umfang von 352 cm. Was ist der Radius der Münze?
Diskussion:
K = 352 cm
Beantwortet:
K = 2πr
352 cm = 2 x 22/7 x r
352 cm = 44 / 7x r
352 cm x 7 = 44 r
r = 2,464 cm / 44
r = 56 cm
5.

Ein Kreis hat eine Fläche von 78,5 cm². Was ist der Umfang des Kreises?
Diskussion:
L = 78,5 cm²
Beantwortet:
L = πr²
78,5 cm² = 3,14 x r²
r² = 78,5 cm² / 3,14
r² = 25 cm²
r = 25 cm²
r = 5 cm
K = 2πr
K = 2 × 3,14 × 5 cm
K = 31,4 cm
6. Ein Kreis hat eine Fläche von 804 cm². Was ist der Umfang des Kreises?
Diskussion:
L = 804 cm²
Beantwortet:
L = πr²
804 cm² = 3,14 x r²
r² = 804 cm² / 3,14
r² = 256 cm²
r = 256 cm²
r = 16 cm
K = 2πr
K = 2 · 3,14 · 16 cm
K = 100,48 cm
7. Die Speichen eines Rades sind 25 cm. Das Rad dreht sich 200 Mal. Wie viele Meter lang war das Rad?
Diskussion:
r = 25 cm
Anzahl der Umdrehungen = 200 mal
Beantwortet:
K = 2πr
K = 2 · 3,14 · 25 cm
K = 157 cm
Die Länge der vom Rad zurückgelegten Spur = Anzahl der Umdrehungen x Radumfang = 200 mal x 157 cm = 31.400 cm = 314 m
8. Ein rundes Kinderspielzeug mit einem Durchmesser von 64 cm. Was ist der Umfang des Spielzeugs?
Diskussion:
d = 64 cm
Beantwortet:
K = πd
K = 3,14 x 64 cm
K = 200,96 cm
9. Andi geht zu einer Gemäldeausstellung. Dort sieht Andi ein kreisförmiges abstraktes Gemälde. Andi hat es auch gemessen. Es stellte sich heraus, dass der Umfang des abstrakten Gemäldes 7.700 cm betrug. Was ist der Radius des kreisförmigen abstrakten Gemäldes?
Diskussion:
K = 7.700 cm
Beantwortet:
K = 2πr
7.700 cm = 2 x 22/7 x r
7.700 cm = 44/7 cm x r
44 r = 7.700 cm × 7
r = 53.900 cm / 44
r = 1.225 cm
10. Ein rundes Glas hat eine Fläche von 9.856 cm². Was ist der Umfang des Kreises?
Diskussion:
L = 9.856 cm²
Beantwortet:
L = πr²
9.856 cm² = 22/7 x r²
22 r² = 9.856 cm² · 7
22 r² = 68.992 cm²
r² = 68.992 cm² / 22
r = √3,136 cm²
r = 56 cm
K = 2πr
K = 2 · 22/7 · 56 cm
K = 352 cm
11. Berechnen Sie den Umfang des folgenden Kreises!
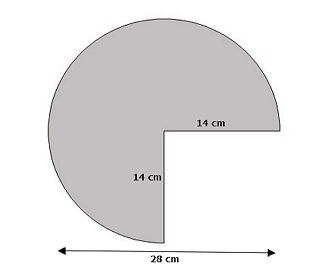
Diskussion:
d = 28 cm
r = 14 cm
Beantwortet:
Der Umfang ist die Summe aller Umrisse in einer Ebene. Das Kreisbild oben sieht also wie folgt aus:
K = 3/4 πd + 2r
K = (3/4 × 22/7 × 28) cm + (2 × 14) cm
K = (3/4 × 88) cm + 28 cm
K = 66 cm + 28 cm
K = 94 cm
12 Es gibt ein kreisförmiges Schwimmbad mit einem Radius von 9,5 m und einen Fußweg außerhalb des Teiches von bis zu 0,5 m Breite. Während einer Aufwärmübung rannte Dada zehnmal um den Pool herum. Wie viele Meter hat er den Pool umrundet?

Diskussion:
Schwimmradius = 9,5 m
Die Breite des Weges = 0,5 m
Beantwortet:
Gesamtdurchmesser = (2 × 9,5 m) + (2 × 0,5 m) = 19 m + 1 m = 20 m
K = πd
K = 3,14 · 20 m
K = 62,8 m
Da Dadang zehnmal herumlief, betrug die zurückgelegte Strecke 10 x 62,8 m = 628 m
13 Vater fuhr ein Auto über eine Strecke von 2.640 m. Während der Fahrt drehte sich Papas Autorad 1000 Mal. Wie viele Zentimeter Umfang und Radius haben Sie?
Diskussion:
Die zurückgelegte Strecke = 2.640 m = 264.000 cm
Anzahl der Windungen = 1000 mal
Beantwortet:
K = zurückgelegte Strecke: Anzahl der Umdrehungen
K = 264.000 cm: 1000-mal
K = 2,64 cm
Die Länge der Räder der Räder meines Autos, die sind:
K = 2πr
264 cm = 2 x 22/7 x r
264 cm = 44/7 r
264 cm x 7 = 44 r
r = 1,848 cm: 44
r = 42 cm
14. Ein kreisförmiger Blumengarten mit einer Fläche von 616 m². Rund um den Park werden alle 4 m immergrüne Bäume gepflanzt. Wie viele immergrüne Bäume können im Blumengarten gepflanzt werden?
Diskussion:
L = 616 m²
Beantwortet:
L = πr²
616 m² = 22/7 x r²
22 r² = 616 m² x 7
22 r² = 4.312 m²
r² = 4.312 m² / 22
r = √196 m²
r = 14 m
K = 2πr
K = 2 · 22/7 · 14 m
K = 88 m
Da der Park alle 4 m von Kiefern umgeben ist, beträgt die Anzahl der Bäume 88 m: 4 m = 22 Bäume
15. Berechnen Sie den Umfang des folgenden Kreises!

Diskussion:
d = 49 cm
Beantwortet:
K = 1/2 πd
K = 1/2 x 22/7 x 49 cm
K = 77 cm
Dies sind einige Beispiele für Fragen und Diskussionen, die ich geben kann. Hoffentlich dieser Artikel über die Formel um den Kreis mit Beispielen für Probleme und deren Diskussion nützlich für euch alle ja. Das ist alles und danke.








