Trapeziumformule (oppervlakte en omtrek) met voorbeeldvragen + discussie

U moet de telactiviteit sindsdien hebben gedaaneerst toen ik een peuter was tot nu toe. Omdat tellen altijd gebeurt in ieders leven, is het geen wonder dat wiskunde een vak is geworden dat al sinds de kleuterschool wordt onderwezen.

Natuurlijk is de moeilijkheidsgraad van wiskundelessen op elk onderwijsniveau verschillend. Uniek is dat wiskunde altijd een onderwerp is dat iemands intelligentie bepaalt.

Hoe beter je wiskundige cijfers bentzal in toenemende mate worden beschouwd als een slim persoon. Misschien is dit ook gebaseerd op het feit of er wiskundige problemen zijn die heel moeilijk te doen zijn. Zodat wiskundigen vaak als genieën worden beschouwd.

Trapeziumformule

De definitie van trapezium is een vormplat dat twee dimensies heeft en is gerangschikt door 4 zijden die evenwijdig maar niet even lang zijn. Trapezium wordt ook gevormd uit 4 ribben waarbij 2 ribben ook evenwijdig aan elkaar zijn maar verschillende lengtes hebben. Trapeziumvormig gebouw heeft verschillende kenmerken die het onderscheiden van andere gebouwen, waaronder:

1. Heeft 1 spelsymmetrie
2. Zorg voor een stompe hoek van minimaal 1 hoek
3. Heeft 4 hoekpunten
4. Heeft 2 zijden parallel aan verschillende lengtes
5. Trapezium is een platte vorm met 4 zijden of vierzijdig

Over trapezium gesproken, natuurlijk heb je datweet of voor het berekenen van de oppervlakte en omtrek van een trapezium een ​​formule nodig is. De formules van het gebied en de omtrek van de trapezium zijn als volgt:

A. Trapeziumvormige brede formule

De brede formule voor trapezium in het algemeen is:

Gebied = ½ × aantal parallelle ribben × hoogte

De bovenstaande formule kan echter worden gewijzigd en aangepastmet trapeziumvorm. Er zijn 3 vormen van trapezium, namelijk juiste trapezium, gelijkbenige trapezium en gewoon elke trapezium. Uitleg van de formule om de oppervlakte van de drie soorten trapezium te berekenen is:

1. De brede formule van de elleboogtrapezium

Zoals de naam al doet vermoeden, is het een rechthoekige trapeziumeen trapeziumvorm met twee rechte hoeken of zijden die parallel en loodrecht op elkaar staan ​​ter hoogte van de trapezium. Of je zou kunnen zeggen dat een van de hoeken in de trapezium van een rechterelleboog een grote 90 ° heeft.

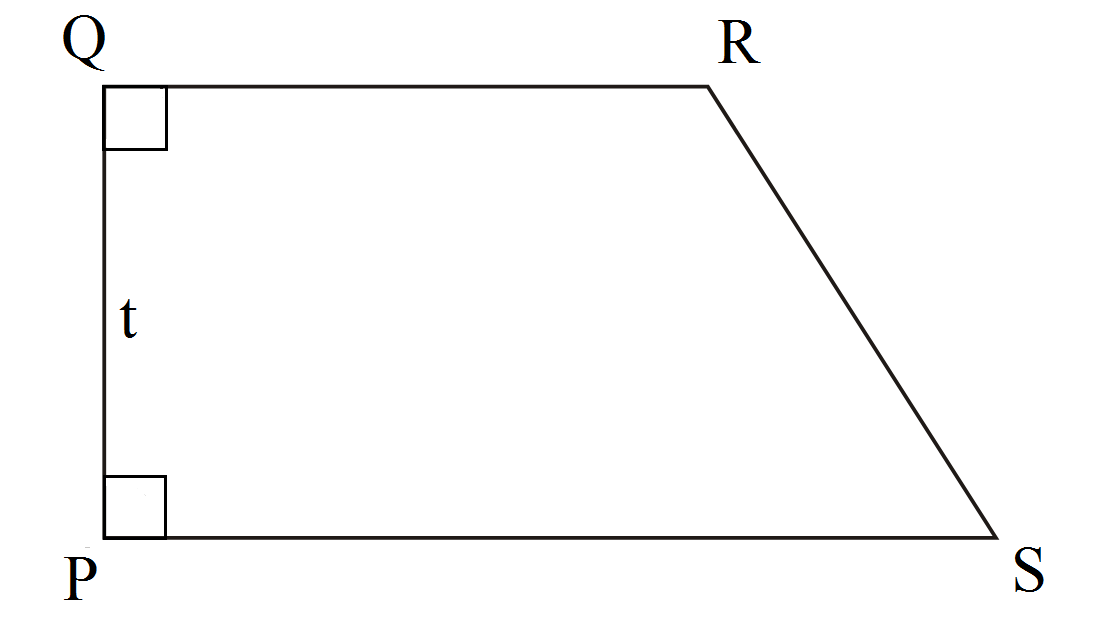
Brede formule voor trapezoïde rechte hoek PQRS: (PQ + RS) × t / 2

2. Gelijkbenige trapeziumvormige brede formule

Naast de rechthoekige trapezium, type wakede andere trapezium is een gelijkbenige trapezium. Waar de gelijkbenige trapezium is een trapezium die een kant van vouwsymmetrie en ribben van dezelfde lengte en uitlijning heeft. Voor meer details zie je op de foto hierboven.

KLMN gelijkbenige trapezium brede formule: (LM + KN) × t / 2

3. Elke brede trapeziumformule

Van de foto hierboven weet je het natuurlijk alwaarom deze trapezoïde zomaar een trapezium wordt genoemd. Dit komt omdat in elke ABCD-trapezoïde hierboven helemaal geen vouwsymmetrie is. Zelfs de maat van de ribben is niet even lang en onregelmatig.

Elke ABCD-trapeziumformule: (BC + AD) × t / 2

B. De trapeziumformule

Om dan de omtrek van een trapezium te achterhalenU moet eerst de formule rond de trapezium gebruiken. Omdat de trapeziumgebiedformule alleen kan worden gebruikt om het gebied te bepalen, en de trapeziumomtrekformule wordt gebruikt om de omtrek van elk type trapezium te bepalen.

De trapeziumformule: AB + BC + CD + DA

Uit bovenstaande formule kan worden afgeleid of de omtrek van de trapezium wordt verkregen uit de som van alle zijden van een trapeziumstructuur.

1. De formule voor de trapezoïde elleboog

In de juiste trapezium is er ook een omtrekformule, namelijk:

Rond de trapeziumelleboog PQRS = PQ + QR + RS + SP

2. De formule voor het reizen rond gelijkbenige

Terwijl de formule rond de gelijkbenige trapezium is:

Rond de trapezoïde gelijkbenige KLMN = KL + LM + MN + NK

3. Alles rondom de trapeziumformule

In principe is de formule rond een trapezium met verschillende soorten hetzelfde. De omtrekformule voor een willekeurige trapezium is:

Willekeurig Alles rond ABCD = AB + BC + CD + DA

Vanaf de derde formule verschillende reisformulesbij het bouwen van het bovenstaande trapezium kan worden geconcludeerd, ongeacht de vorm van het trapezoïde, blijft de omtrekformule één. Maar in de trapezium is er niet alleen een brede en cirkelvormige formule, maar er is een formule die de stelling van Pythagoras gebruikt, speciaal voor rechthoekige trapezines. De formule is:

Hoge hoek trapeziumformule

Formule schuin aflopend (c) rechter trapezium

Formule aan de basiszijde (a) rechter trapezium

Nou, dat was een voorbeeld van een trapeziumprobleem en een complete discussie. Ik hoop dat het nuttig voor je is.