Wzór na budowę przestrzeni i przykłady pytań i dyskusji

Pewnie często słyszałeś słowo „budzę się”przestrzeń podczas nauki matematyki w szkole. Rodzaje różnych rodzajów budynków. Przestrzeń budowlaną można interpretować jako obiekt lub pokój o trójwymiarowym kształcie, który ma zarówno zawartość, jak i objętość oraz ma granice (boki).

Nie kompilacja przykładowym runag jest kostki, belki, trójkątne pryzmaty, prostokątna piramida, trójkątna piramida, stożki, rurki i kule.

Każdy budynek ma powierzchnię i piłkę. Aby lepiej zrozumieć formułę używaną do jej znalezienia, Fuj wysłuchałem wyjaśnienia wzoru na budowę przestrzeni i przykładów problemu poniżej:

Formuła budowy przestrzeni

1. Kostka

Co to jest sześcian? Kostka jest budować przestrzeń the płaska strona, gdzie wszystkie żebra są tej samej długości jak również wszystkie boki o kwadratowym kształcie. Na przykład kości, rubik, tektura i inne.

Przed omówieniem formuły runag najpierw dowiedz się, jaka jest natura kostki? Oto natura sześcianu:

Przesiać właściwości kostki:

• Wszystkie boki sześcianu są prostokątne
• Ma 8 wierzchołków
• Ma 12 żeber o tej samej długości
• Ma 12 płaszczyzn ukośnych (boczne przekątne) o tej samej długości
• Ma 4 przekątne o tej samej długości
• Ma 6 elementów bocznych
• Ma 6 prostokątnych pól po przekątnej

Ponieważ sześcian jest przestrzenią budowlaną, oczywiście są rzeczymusimy obliczyć, podobnie jak objętość lub pole powierzchni. Oto kilka formuł, których można użyć do rozwiązania problemów w kostce:

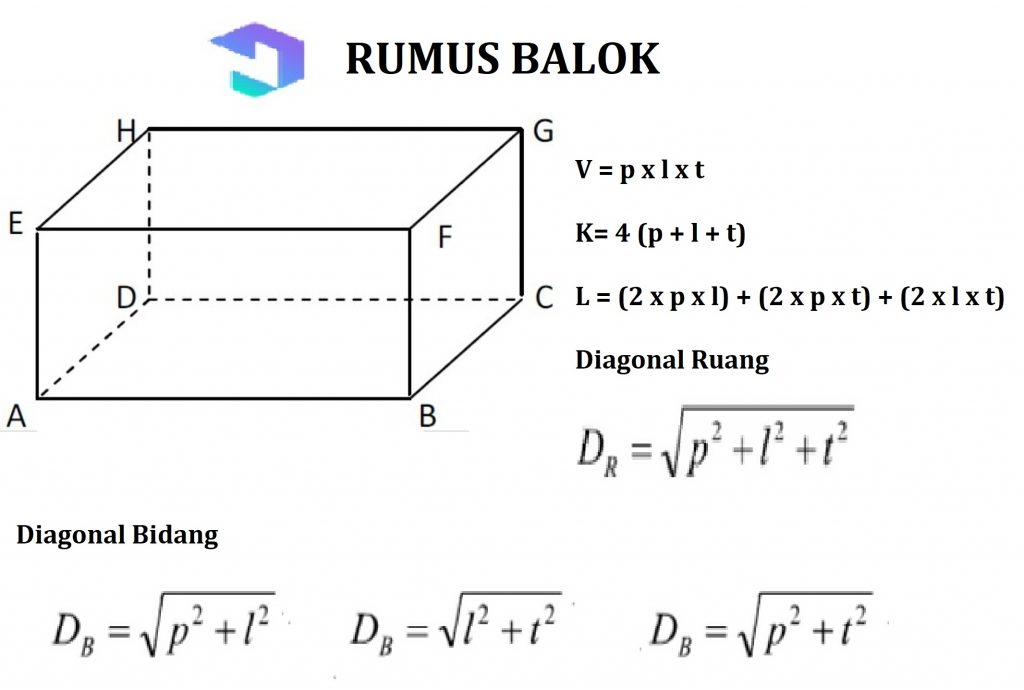
2. Belki

Zbuduj płaski boczny pokój drugi to wiązka, z 3 pary boków o rozmiarze i kształcie jak również stawić czoła sobie. Prostokątny kształt boku.

Właściwości wiązki:

• Ma bok o długim kształcie persengi
• Posiadające żebra równoległe do tego samego rozmiaru
• Mają przekątne skierowane do siebie i tej samej długości
• Ma taką samą długość przekątnej

3. Pryzmaty trójkątne

Pryzmat jest budować przestrzeń kto ma pole cokołu i górne pole the przystający i równolegle. Powód, dla którego jest przystający i równy, tak ponieważ druga strona pryzmatu jest wyprostowana, a kształt ma jajargenjang lub prostokąt. Przystający jest przystający i równy.

Istnieje kilka rodzajów pryzmatów, takich jak pięciokątny, czworokątny i trójkątny. To, co go wyróżnia, to liczba form podstawy i dachu.

Właściwości trójkątnego pryzmatu:

• Ma 3 przystające dachy i podstawy.
• Każda strona boku przypomina drabinę i jest prostokątna
• Zazwyczaj mają żebra pionowe (niektóre nie są pionowe)
• Każda płaszczyzna ukośna po tej samej stronie ma ten sam rozmiar

Do wyznaczania pola powierzchni, objętości trójkątnych pryzmatów powszechnie stosuje się następujące wzory:

4. Limity czworoboczne

Piramida czworoboczna jest budować przestrzeń kto ma podstawa w kształcie prostokąta. Zwykle piramida ma płaszczyznę boczną, która jest wyprostowana i trójkątna, i spoczywa w jednym punkcie, ponieważ przecina się.

Poniżej znajdują się wzory, które można zastosować w czworobocznej piramidzie:

5. Trójkątne limy

Trójkątne limy jest budować przestrzeń kto ma trójkątna podstawa. Zwykle piramida ma pionową płaszczyznę bocznąi mają kształt trójkąta i spoczywają na jednym punkcie, ponieważ przecinają się. To, co wyróżnia nazwę piramidy, to kształt podstawy, którą pokrywa, na przykład pięciokątna piramida, czworokątna piramida i trójkątna piramida.

Poniżej znajdują się formuły, których można użyć w piramidzie:

6. Szyszki

Stożek to pokój z profilowaną podstawąkoło i ma koc z płaszczyzny bocznej i jest uformowany z koła jak klin. Często rolnicy muszą zobaczyć czapki urodzinowe lub czapki z daszkiem. Nie jest to przykład kształtu stożka.

Charakterystyka szyszek:

• Mają 2 żebra
• Posiadanie wierzchołka jako spotkania wierzchołka
• Ma 2 płaszczyzny boczne (boki koła składają się z jednego i jako podstawy i jednego pola kocowego)

Poniżej znajdują się formuły, które można wykorzystać w rozwiązywaniu problemów w konstrukcji przestrzeni stożkowej:

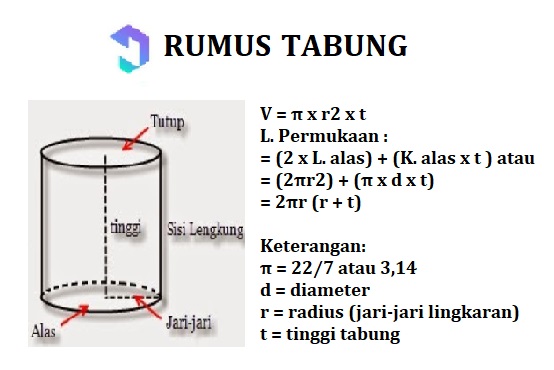
7. Rurka

Rura jest budować przestrzeń składający się z podstawa i pokrycie w kształcie koło, a także mając zakrzywiony kocz boku prostokąt.

Właściwości tuby:

• Miej matę i pokrywkę tego samego rozmiaru
• Mają 2 żebra
• Ma 3 pola (2 kółka i 1 prostokąt)
• Nie mam wierzchołka

Ogólny wzór do obliczania powierzchni i objętości rur:

8. Piłka

Bardzo często widzimy piłkę w życiu codziennym, nawet niektórzy z was naprawdę lubią gry w piłkę. Tak piłka budzi przestrzeńmają powierzchnię, a także objętość. Odnosi się to również do tego, dlaczego piłkę można łatwo dryblować i kontrolować, ponieważ dwie rzeczy są odpowiedzią.

Właściwości piłki:

• Nie ma wierzchołków i żeber
• Mieć taką samą odległość do środka w punkcie łuku.

Oto wzór na znalezienie objętości i pola powierzchni kuli:

Przykładowe pytania + dyskusja

1. Rubik ma długość boku 5 cm. Jaka jest objętość rubika?

Odpowiedź:

V = s x s x s

= 5 x 5 x 5

= 125

Więc objętość rubika 125 cm³

2. Blok ma długość 8 cm, szerokość 5 cm i wysokość 4 cm. Jaki jest obwód bloku?

K = 4 (p x l x t)

= 4 (8 x 5 x 4)

= 640

Tak więc obwód wiązki jest 640 cm

3. Dowiedz się, jaka jest objętość trójkątnego pryzmatu, jeśli powierzchnia podstawy wynosi 16 cm, a wysokość 10 cm!

Odpowiedź:

V = podstawa L x t

= 16 x 10

= 160

Więc objętość 160 cm²

4. Obliczyć objętość prostokątnej piramidy, jeśli ma ona 6 cm długości, 4 cm szerokości i 9 cm wysokości

Odpowiedź:

V = 1/3 (p x l x t)

= 1/3 (6 x 4 x 9)

= 71

Tak więc objętość prostokątnej piramidy jest 72 cm²

5. Obliczyć objętość piramidy trójkąta, jeśli powierzchnia podstawy wynosi 24 cm, a wysokość 5 cm?

Odpowiedź:

V = 1/3 (podstawa L x t)

= 1/3 (24 x 5)

= 40

Więc powierzchnia jest 40 cm²

6. Kapelusz urodzinowy ma promień 7 cm, jaka jest jego podstawa?

Odpowiedź:

Podstawa L = πr²

= 7/22 x 7²

= 154

Tak szeroki kapelusz urodzinowy jest 154 cm

7. Promień rury wynosi 15 cm. Jeśli wysokość wynosi 20 cm, objętość rurki wynosi ...

Odpowiedź:

V = πr²t

= 3,14 x 15² x 20

= 14,130

Więc objętość tuby jest 14 130 cm²

8. Koło roweru ma promień 14 cm. Określ powierzchnię koła roweru!

Odpowiedź:

L = 4πr²

= 4 x 22/7 x 14²

= 2464

Tak więc powierzchnia kół rowerowych, których szprychy wynoszą 14 cm, wynosi 2464 cm²

To jest dyskusja na temat formuły przestrzeni budowlanej (powierzchnia i objętość każdej przestrzeni budowlanej) wraz z przykładowymi problemami i dyskusją. Mam nadzieję, że przydatne i łatwe do zrozumienia!