Fórmula para volume de cubos e área de superfície de cubos e exemplos de problemas

Anteriormente, discutimos sobre fórmulaso volume do tubo, ainda discutindo sobre a construção de espaço, desta vez discutirá a fórmula para encontrar o volume do cubo. O cubo é um edifício com 12 nervuras de frutas do mesmo comprimento e é composto por 6 lados com a forma de um quadrado

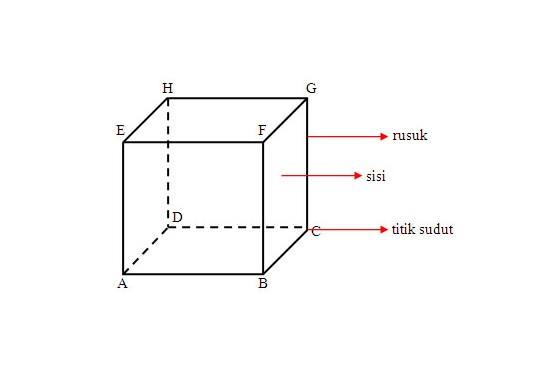
O cubo geralmente possui partes, a saber: plano lateral, nervura, plano diagonal, vértice, lado diagonal e espaço diagonal. Da mesma forma, os outros cubos que têm um volume loh. Para mais detalhes, vamos considerar a explicação abaixo!

Fórmulas de volume de cubo

Antes de discutir o volume de um cubo, primeiro discutimos os elementos relacionados ao seu volume.

Campo / Lado

A área / lado do cubo é algo que é um limite no cubo. Nah, o cubo tem 6 lados que têm o mesmo comprimento na forma de um quadrado.

Parte do lado do cubo:

Lado superior (EFGH)
Lado inferior (ABCD)
Lado frontal (ABFE)
Lado traseiro (DCGH)
Lado direito do lado (ADHE)
Lado esquerdo (BCGF)

Costelas

As linhas do cubo Pda que têm interseções entre 2 campos / lados são chamadas de nervuras. Na figura acima, as nervuras do cubo incluem AB, AE, BC, BF, CD, CG, DA, DH, EF, HE, FG, GH.

Vertex

O ponto de intersecção entre 2 ou 3 nervuras no cubo é chamado de ponto sudur. Com base na figura acima, o cubo consiste em 8 ângulos, A, B, C, D, E, F, G, H.

Lado diagonal / plano diagonal

Se houver uma linha longa em cada cantoo cubo virado será formado como um triângulo igual. A linha é um lado ou plano diagonal. Com base na imagem do cubo acima, existem 12 lados / campos diagonais, nomeadamente AC, AF, AH, BD, BE, BG, CH, DE, DG, EG, FC e HG.

Espaço diagonal

Uma linha em um espaço se tornaa conexão entre dois pontos um de frente para o outro é chamada de diagonal do espaço. Com base na figura do cubo acima, existem 4 espaços diagonais, nomeadamente as linhas AG, BH, DF e EC.

Plano diagonal

Um campo formado de 2 linhaslado / plano diagonal e 2 nervuras paralelas denominadas plano diagonal. Com base na imagem do cubo acima, existem 4 campos diagonais, nomeadamente ABGH, ACGE, DBFH, EFCG.

Nah, depois de reconhecer o cubo a seguir, discutimos a fórmula para encontrar o volume sim Considere a fórmula abaixo:

A fórmula do volume do cubo e a área de superfície de um cubo

Exemplos de perguntas e discussão

A seguir, explicaremos algumas questões relacionadas ao volume do tubo acabado vamos lá assisti atentamente para você entender!

1. Um cubo com nervuras de 15 cm de comprimento. Calcule o volume do cubo!

Resposta:

s = 15 cm

Volume do tubo

V = s³
= 15 cm x 15 cm x 15 cm
= 3375 cm³

Então o volume do cubo é 3375 cm³

2. Se o volume do cubo for 343 cm³. Qual é o comprimento lateral do cubo?

Resposta:

V = 343 cm³

então, V = s³
343 cm³ = s³
s = ∛343
s = 7 cm

Então O cubo tem um comprimento Lado de 7 cm.

3. Um rubik tem um lado de 5 cm. Determinar o volume do rubik?

Resposta:

V = s³
= 5 cm x 5 cm x 5 cm
= 125 cm³

Então o volume do rubik é 125 cm³

4. Se o comprimento da braçadeira for 20 cm. Qual é o volume do cofre?

Resposta:

V = lado x lado x lado
V = 20 cm x 20 cm x 20 cm
V = 8000 cm³

Então o volume do cofre é 8000 cm³

5. Uma banheira possui nervuras de 2,5 cm de comprimento, quanta água pode encher a banheira?

Resposta:

V = lado x lado x lado
V = 2,5 m x 2,5 m x 2,5 m
V = 15.625 m³

Então é necessária muita água para que uma banheira cheia 15.625 m³

6. O volume de uma caixa em forma de cubo é de 729 cm³. Calcular qual é o comprimento total da nervura da caixa?

Resposta:

V = s³
729 = s³
s³ = 729
s = 29729
s = 9 cm

Número de nervuras do cubo = 12
Número total de costelas = 9 x 12 = 108 cm

Então o comprimento total das costelas da caixa 108 cm.

7 Andi despejou água em uma banheira em forma de cubo com um comprimento de costelas de 14 cm. Mas a quantidade de água derramada por Andi era apenas metade da bacia. Quanta água Andi derramou?

Resposta:

Volume de água no banho = volume ½ cubo
Volume de água na banheira = ½ x s³

= ½ x 14 cm x 14 cm x 14 cm

= ½ x 2.744 cm³

= 1.372 cm³

Então a quantidade de água que Andi derramou é 1.372 cm³.

8. O comprimento das costelas do cubo é de 12 cm. em seguida, corte em cubos com um tamanho pequeno, com nervuras de 3 cm de comprimento. Determinar quantos cubos pequenos são produzidos?

Resposta:
O volume do cubo grande = 12 cm x 12 cm x 12 cm = 1.728 cm³
O volume do cubo pequeno = 3 cm x 3 cm x 3 cm = 27 cm³
O número total de cubos pequenos = 1.728: 27 = 64

Então a soma de todos os cubos pequenos após o corte é 64 peças

9. Qual é a área diagonal de um cubo se a caixa torácica tiver 24 cm de comprimento? (dik: √2 = 1.414)

Resposta:

Área da área diagonal = 24 cm x 24 cm x √2

= 10 cm x 10 cm x 1.414

= 814.464 cm²

Então a área da diagonal é 814.464 cm²

10. Uma caixa em forma de cubo com nervuras de 10 cm e depois cortada em pequenas caixas cúbicas com um volume de 500 cm³Conte quantos cubos pequenos você tem no total!

Resposta:

O volume da caixa grande (cubo) = 10 cm x 10 cm x 10 cm = 1.000 cm^{3 </ sopa

O volume do cubo pequeno = 500 cm^{3 </ sopa}}

Número de cubos pequenos = volume de cubos grandes: volume de cubos pequenos
O número de cubos pequenos = 1.000: 500 = 2 peças

Então a soma de todos os cubos pequenos após o corte é 2 peças

Nah, das perguntas e discussões acima, esperoVocê pode entender facilmente como resolver problemas se eles estiverem relacionados à fórmula para a construção de um cubo. Por uma questão de simplicidade, você deve memorizar a fórmula primeiro e depois entender o objetivo do problema e o que é conhecido no problema.