Vzorec pre budovanie priestoru a príklady otázok a diskusií

Museli ste počuť slovo prebudiť sa častopriestor pri štúdiu matematiky v škole. Druhy rôznych typov budov. Priestor budovy možno interpretovať ako objekt alebo miestnosť s trojrozmerným tvarom, ktorý má obsah aj objem a má hranice (strany).

No, príklad zostavenia runag je kocky, trámy, trojuholníkové hranoly, pravouhlá pyramída, trojuholníková pyramída, kužele, rúrky a gule.

Každá budova má plochu a guľu. Ak chcete lepšie porozumieť vzorcu použitému na jeho nájdenie, ísť napred Vypočuli sme si vysvetlenie vzorca pre výstavbu priestoru a príklady problému nižšie:

Vesmírna zostava vzorec

1. Kocka

Čo je kocka? Kocka je a vybudovať priestor ktorý plochá strana, kde všetky rebrá majú rovnakú dĺžku ako aj všetky strany štvorcového tvaru. Napríklad kocky, rubik, kartón a ďalšie.

Predtým, ako budete diskutovať o runovej formule, najprv vedzte, aká je povaha kocky? Tu je podstata kocky:

Preosiať vlastnosti kocky:

• Všetky strany kocky sú pravouhlé
• Má 8 vrcholov
• Má 12 rebier rovnakej dĺžky
• Má 12 diagonálnych rovín (bočné uhlopriečky) rovnakej dĺžky
• Má 4 uhlopriečky rovnakej dĺžky
• Má 6 bočných kusov
• Má 6 obdĺžnikových diagonálnych polí

Pretože kocka je stavebným priestorom, samozrejme existujú vecimusíme počítať, podobne ako objem alebo plocha povrchu. Tu je niekoľko vzorcov, ktoré môžete použiť na riešenie problémov v kocke:

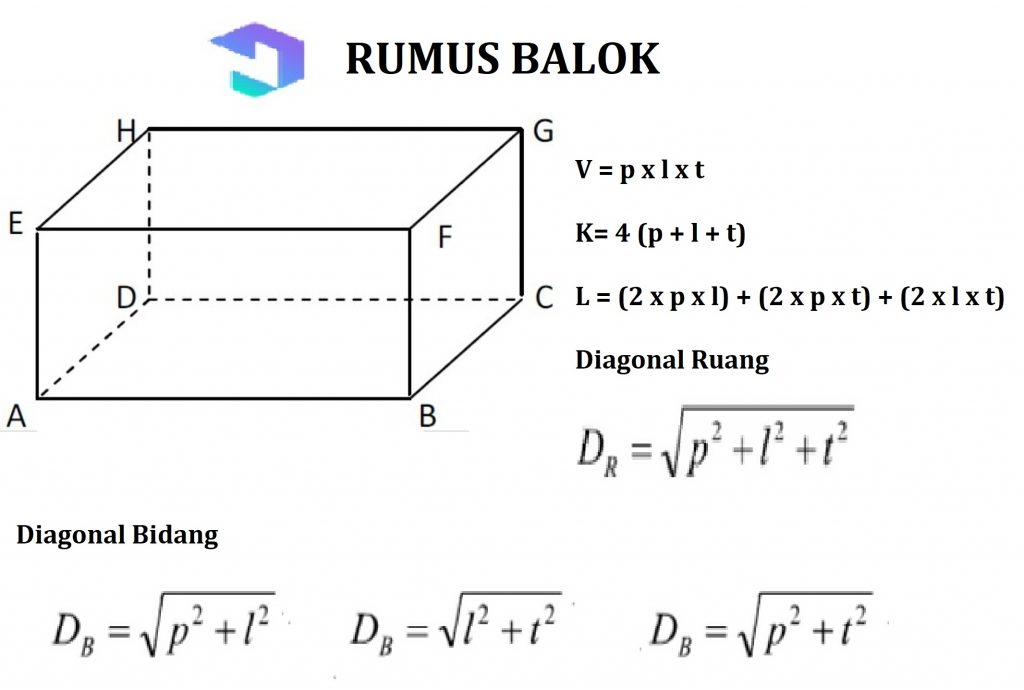
2. Nosníky

Postavte byt na bočnej strane druhým je lúč s 3 páry strán s veľkosťou a tvarom ako aj čeliť k sebe, Obdĺžnikový bočný tvar.

Vlastnosti lúča:

• Mať stranu s dlhým tvarom persengi
• Majú rebrá rovnobežné s rovnakou veľkosťou
• Majú diagonály oproti sebe a rovnakú dĺžku
• Má diagonálny priestor rovnakej dĺžky

3. Trojuholníkové hranoly

hranol je vybudovať priestor kto má podstavec poľa a horné pole ktorý zhodný a paralelné, Dôvod, prečo je zhodný a rovnaký, áno pretože druhá strana hranolu je zvislá a tvar je jajargenjang alebo obdĺžnikový. Zhoda je zhodná a rovnaká.

Existuje niekoľko druhov hranolov, ako je päťuholníkový hranol, štvoruholníkový hranol a trojuholníkový hranol. To, čo ho odlišuje, je počet foriem podstavca a strechy, ktoré má.

Vlastnosti trojuholníkového hranolu:

• Má 3 zhodné strechy a základne.
• Každá strana je ako rebríkový rebrík a obdĺžnikový
• Spravidla majú zvislé rebrá (niektoré nie sú zvislé)
• Každá diagonálna rovina na tej istej strane má rovnakú veľkosť

Nasledujúce vzorce sa bežne používajú pri hľadaní povrchovej plochy, objemu trojuholníkových hranolov:

4. Štvorstranný Limas

Štvorstranná pyramída je a vybudovať priestor kto má obdĺžnikový tvar základne. Pyramída má zvyčajne bočný povrch, ktorý je vzpriamený a trojuholníkový a spočíva v jednom bode, pretože sa pretína.

Nasledujú vzorce, ktoré sa dajú použiť v štvoruholníkovej pyramíde:

5. Trojuholníkové limá

Trojuholníkové limy je a vybudovať priestor kto má trojuholníková základňa. Pyramída má zvyčajne zvislú bočnú rovinua majú trojuholníkový tvar a spočívajú na jednom bode, pretože sa pretínajú. Názov pyramídy sa odlišuje tvarom základne, ktorú pokrýva, napríklad päťuholníkovej pyramídy, štvoruholníkovej pyramídy a trojuholníkovej pyramídy.

Nasledujú vzorce, ktoré je možné použiť v pyramíde:

6. Kužele

Kužeľ je miestnosť s tvarovanou základňoukruh a má bočnú rovnú pokrývku a je vytvorená z kruhu ako klin. Pre poľnohospodárov musíte často vidieť klobúky narodeniny alebo čiapky. No, je to príklad tvaru kužeľa.

Vlastnosti kužeľov:

• Majú 2 rebrá
• Mať vrchol ako stretnutie vrcholu
• Má 2 kusy bočných rovín (bočné strany kruhu pozostávajú z jednej a ako základne a jedného plošného poľa)

Nasledujú vzorce, ktoré sa dajú použiť pri riešení problémov pri konštrukcii kužeľového priestoru:

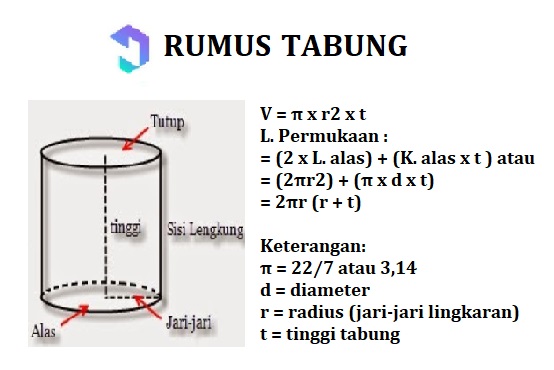
7. Trubica

Rúrka je a vybudovať priestor pozostávajúce z základňa a kryt v tvare kruh, ako aj mať zakrivená deka, zo strany obdĺžnik.

Vlastnosti trubice:

• Majte rohož a veko rovnakej veľkosti
• Majú 2 rebrá
• Má 3 polia (2 kruhy a 1 obdĺžnik)
• Nemáte vrchol

Všeobecný vzorec na výpočet plochy a objemu rúrok:

8. Lopta

Loptičku často vidíme v každodennom živote, dokonca niektorí z vás majú radi loptové hry. Jo, lopta je taká, ktorá prebúdza priestormajú povrchovú plochu a tiež objem. To tiež súvisí s tým, prečo je možné loptu ľahko driblovať a ovládať, pretože dve veci sú odpoveďou.

Vlastnosti lopty:

• Nemá vrcholy ani rebrá
• Majte rovnakú vzdialenosť od stredu v bode krivky.

Nasleduje vzorec na nájdenie objemu a plochy povrchu gule:

Príklad otázok + diskusia

1. Rubik má dĺžku strany 5 cm. Aký je objem rubiku?

odpoveď:

V = s x s x s

= 5 x 5 x 5

= 125

Takže objem rubiku 125 cm³

2. Blok má dĺžku 8 cm, šírku 5 cm a výšku 4 cm. Aký je obvod bloku?

K = 4 (p x l x t)

= 4 (8 x 5 x 4)

= 640

Takže obvod lúča je 640 cm

3. Zistite, aký je objem trojuholníkového hranolu, ak je základná plocha 16 cm a výška 10 cm!

odpoveď:

V = L báza x t

= 16 x 10

= 160

Takže objem 160 cm²

4. Vypočítajte objem pravouhlej pyramídy, ak je 6 cm dlhá, 4 cm široká a 9 cm vysoká

odpoveď:

V = 1/3 (p x l x t)

= 1/3 (6 x 4 x 9)

= 71

Objem obdĺžnikovej pyramídy je 72 cm²

5. Vypočítajte objem pyramídy trojuholníka, ak je základná plocha 24 cm a výška 5 cm?

odpoveď:

V = 1/3 (základňa x t)

= 1/3 (24 x 5)

= 40

Takže povrchová plocha je 40 cm²

6. Narodeninová čiapka má polomer 7 cm, čo je jej spodná časť?

odpoveď:

L báza = πr²

= 7/22 x 7²

= 154

Takže široký základný klobúk je 154 cm

7. Polomer rúrky je 15 cm. Ak je výška 20 cm, potom je objem trubice ...

odpoveď:

V = πr²T

= 3,14 x 15² x 20

= 14,130

Takže objem trubice je 14,130 cm²

8. Kolo bicykla má polomer 14 cm. Zistite povrchovú plochu bicykla!

odpoveď:

L = 4πr²

= 4 x 22/7 x 14²

= 2464

Povrch kolies kolies, ktorých lúče sú 14 cm, je teda 2464 cm²

To je diskusia o vzorci pre stavebný priestor (plocha a objem každého stavebného priestoru) doplnená o ukážkové problémy a diskusiu. Dúfajme, že užitočné a ľahko pochopiteľné!