Формула за изградњу простора и примери питања и дискусије

Сигурно сте чули да се реч често пробудипростора током студирања математике у школи. Типови разних типова зграда. Грађевински простор се може тумачити као објект или соба тродимензионалног облика који има и садржај и запремину и има границе (стране).

Не, пример градње рунаг је коцке, греде, троугласте призме, правоугаона пирамида, трокутаста пирамида, стожци, цеви и сфере.

Свака зграда има површину и куглу. Да бисте боље разумели формулу коришћену за његово проналажење, иук слушао објашњење формуле за изградњу простора и примере проблема у наставку:

Спаце Буилд Формула

1. Коцка

Шта је коцка? Коцка је а изградити простор тхе тхе равна страна, где сва ребра су исте дужине као и све стране квадратног облика. На пример коцкице, рубик, картон и друге.

Пре него што размотримо формулу рунаг-а, прво знате која је природа коцке? Па, ево природе коцке:

Просијте својства коцке:

• Све стране коцке су правоугаоне
• Има 8 врхова
• Има 12 ребара исте дужине
• Има 12 дијагоналних равни (бочне дијагонале) исте дужине
• Има 4 дијагонале исте дужине
• Има 6 бочних комада
• Има 6 правокутних дијагоналних поља

Пошто је коцка простор за изградњу, наравно да постоје ствариморамо израчунати, као запремина или површина. Ево неких формула које можете користити за решавање проблема у коцки:

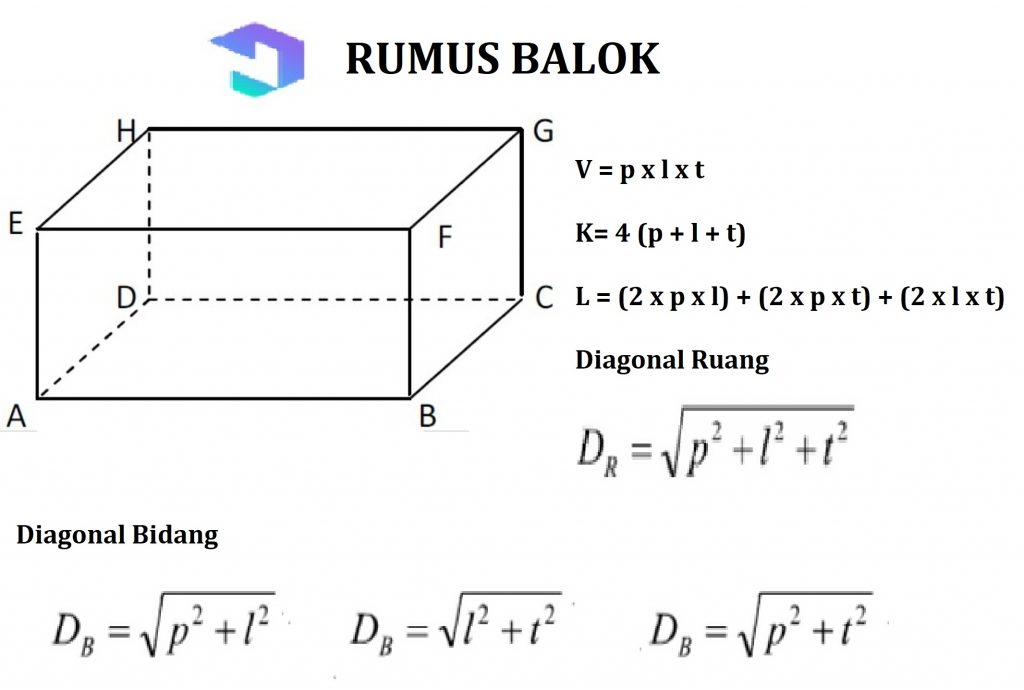
2. Греде

Изградите равну бочну собу други је сноп, са 3 пара страна са величином и обликом као и лицем у лице. Правоугаони бочни облик.

Својства снопа:

• Има страну дуге персенги облика
• Има ребра паралелна исте величине
• Имајте дијагонале окренуте једна према другој и исте дужине
• Има дијагонални простор исте дужине

3. Трокутасте призме

Призма је изградити простор ко има поље за пиједестал и горње поље тхе тхе конгруентна и паралелно. Разлог зашто је уједначен и једнак, да јер је друга страна призме усправна, а облик је јајаргењанг или правоугаоник. Конгруент је конгруентан и једнак.

Постоји неколико врста призми као што су петерокутна призма, четворострана призма и троугласта призма. Оно што га разликује је број облика базе и крова које има.

Својства трокутасте призме:

• Има 3 конгруентна крова и постоља.
• Свака страна је попут мердевина мердевина и правоугаона
• Обично имају усправна ребра (нека нису усправна)
• Свака дијагонална равнина на истој страни има исту величину

Следеће формуле се обично користе за проналажење површине, запремине троугластих призми:

4. Четверострани лимас

Четверострана пирамида је а изградити простор ко има правоугаони облик. Обично пирамида има бочну равнину која је усправног и троугластог облика и почива у једној тачки јер се пресече.

Следе формуле које се могу користити у четверокутној пирамиди:

5. Троугласти лимари

Троугласти лимари је а изградити простор ко има троугласта основа. Обично пирамида има усправну бочну равнинуи су троугластог облика, и почивају на једној тачки јер се пресецају. Оно што разликује назив пирамиде је облик базе коју покрива, као што је пирамида пентагона, четворострана пирамида и троугласта пирамида.

Следе формуле које се могу користити у пирамиди:

6. Конуси

Конус је соба са обликованом базомкруг и има покривач бочне равни и формиран је од круга попут клина. Често морате да видите фармерке и капе за фармере. Не, то је пример облика конуса.

Карактеристике конуса:

• Имајте 2 ребра
• Имати вертекс као састанак вертека
• Има 2 бочне равни (стране круга се састоје од једне и као база и једно покривачко поље)

Следе формуле које се могу користити у решавању проблема у конусној конструкцији простора:

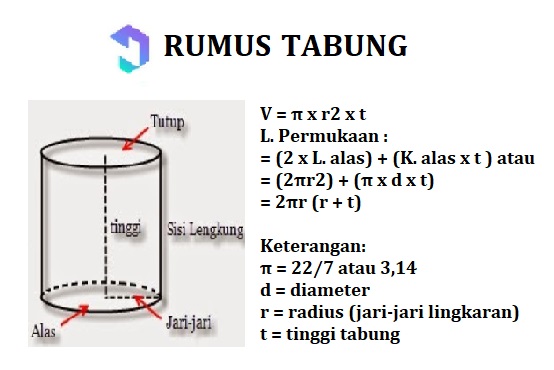
7. Тубе

Цев је а изградити простор који се састоји од постоље и поклопац у облику круг, као и да имају закривљено ћебе, са стране правоугаоник.

Својства цеви:

• Имајте простирку и поклопац исте величине
• Имајте 2 ребра
• Садржи 3 поља (2 круга и 1 правоугаоник)
• Немате вертекс

Општа формула за прорачун површине и запремине цеви:

8. Лопта

Лоптицу врло често виђамо у свакодневном животу, чак неки од вас воле игре са лоптом. Да лопта је та која буди просторимају површину и волумен. Ово се такође односи на то зашто се лопта може лако дриблати и контролисати, јер су две ствари одговор.

Својства куглице:

• Нема врхове и ребра
• Имајте исту удаљеност до центра на месту кривине.

Следећа је формула за проналажење запремине и површине сфере:

Пример питања + Дискусија

1. Рубик има бочну дужину од 5 цм. Колика је запремина рубика?

Одговор:

В = с к с к с

= 5 к 5 к 5

= 125

Дакле, количина рубика 125 цм³

2. Блок је дужине 8 цм, ширине 5 цм и висине 4 цм. Који је обим блока?

К = 4 (п к л к т)

= 4 (8 к 5 к 4)

= 640

Дакле, обим греде је 640 цм

3. Откријте колика је запремина троугласте призме ако је основна површина 16 цм, а висина 10 цм!

Одговор:

В = Л основа к т

= 16 к 10

= 160

Дакле, запремина 160 цм²

4. Израчунајте запремину правоугаоне пирамиде ако је дугачка 6 цм, ширина 4 цм и висина 9 цм

Одговор:

В = 1/3 (п к л к т)

= 1/3 (6 к 4 к 9)

= 71

Дакле, запремина правоугаоне пирамиде је 72 цм²

5. Израчунајте запремину троугласте пирамиде ако је површина основе 24 цм, а висина 5 цм?

Одговор:

В = 1/3 (Л основна к т)

= 1/3 (24 к 5)

= 40

Дакле, површина је 40 цм²

6. Рођендански шешир има пречник од 7 цм, шта је основа шешира?

Одговор:

Л база = πр²

= 7/22 к 7²

= 154

Толико је основни шешир за рођендан 154 цм

7. Радијус цеви је 15 цм. Ако је висина 20 цм, тада је запремина цеви ...

Одговор:

В = πр²т

= 3,14 к 15² к 20

= 14.130

Значи запремина цеви је 14,130 цм²

8. Точак бицикла је радијуса од 14 цм. Одредите површину бициклистичког точка!

Одговор:

Л = 4πр²

= 4 к 22/7 к 14²

= 2464

Дакле, површина бициклистичких точкова чија је жбица 14 цм 2464 цм²

То је расправа о формули за изградњу простора (површина и запремина сваког грађевинског простора), заједно са узорком проблема и дискусијом. Надам се корисно и лако разумљиво!