Samling av trigonometriformler med exempel på frågor och deras diskussion
För er som fortfarande är studentoch de som har arbetat måste ha studerat matematik. Detta ämne har verkligen undervisats för studenter sedan grundskolan fram till studenter vid universitetet.
Till och med matematik ingår alltid i skolprov och nationella prov på flera utbildningsnivåer.
Eftersom detta ämne också är fullt av studentersom ofta klagar när han får en uppgift att göra matematiska problem. Vissa av formlerna i matematiken är tillräckligt för att tappa sinnet för att förstås. En matematisk formel som är ganska svår att lära sig är den trigonometriska formeln.
Samling av trigonometriformler

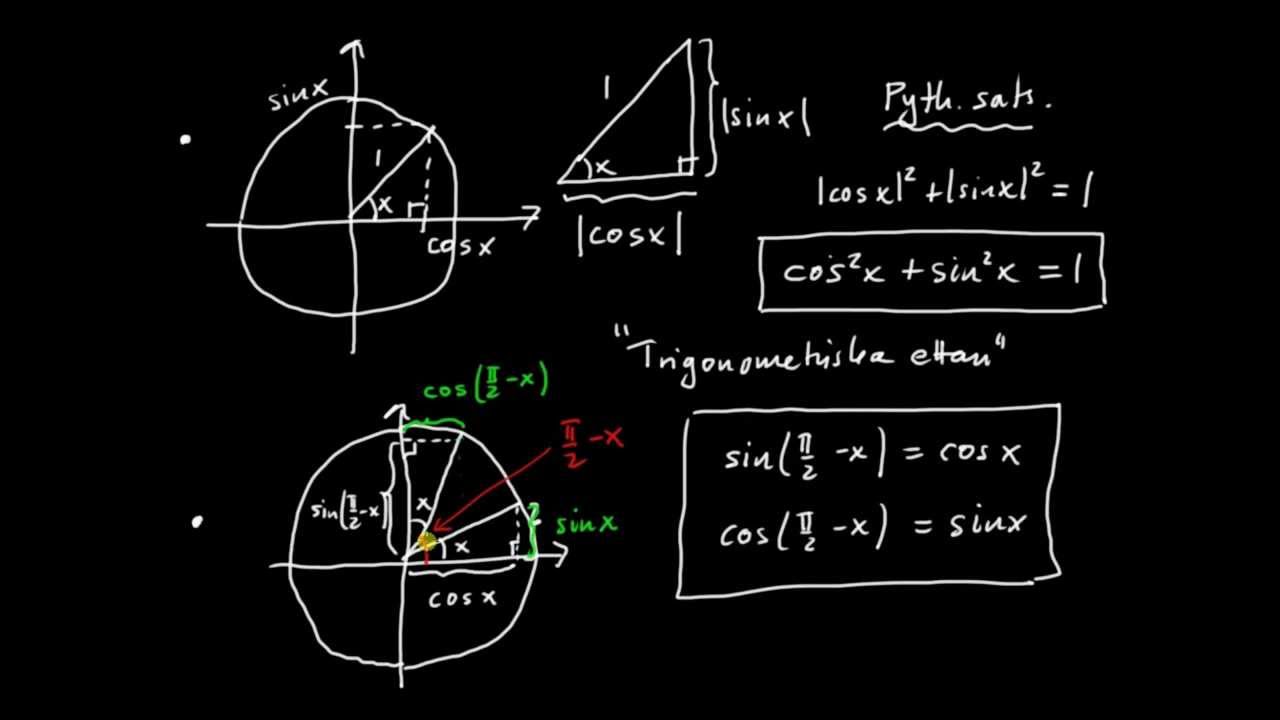
Prata om trigonometriformler då dukommer att lära sig om triangelformer. Eftersom trigonometriformeln är en formel som studerar förhållandet mellan vinklar och sidor som finns i triangelformer. Medan själva den trigonometriska funktionen är indelad i tre, nämligen funktionen av consinus (cos), sinus (sin), secan (sec), tangent (solbränna), cotangen (cotan) och kosekan (cosec).
1. Trigonometry Function Formula
Den första trigonometriska formeln kommer från de trigonometriska funktionerna ovan. Där varje formel har ett sätt att beräkna från varje hörn av triangeln. Den trigonometriska funktionsformeln är

För formeln används sin α för att beräkna sidorfronten dividerad med den avfasade sidan. Medan formeln cos α används för att beräkna sidan dividerad med hypotenusen. Och solbränna α är formeln från framsidan för hypotenusen i triangeln. För att göra det lättare att komma ihåg de tre formelfunktionerna ovan kan du använda följande förkortningar.
SinDeMi
Förkortning av sluttande främre sinus eller sin α-formel.
CosSaMi
Sido sluttande Cosines eller cos α-formel.
TanDeSa
Och förkortningen TanDeSa står för Side Front Tangent eller tan α-formel.
2. Trigonometri-identitetsformler

Den trigonometriska identitetsformeln är en formeljämföra trigonometri med x vinkelvariabler. Där variabeln x erhålls från mått på grader och radianer. Medan sättet att lösa ekvationen sin xº = sin? ° (x? R) är:
Använd först vinkelförhållandet sin (180º -? º) = sin? º och sin (? º + k.360º) = sin? º. Ange sedan ekvationen sin xº = sin? º vara
Om sin x0 = synd?0 (x? R), då:
x =? + k.3600 eller x = (1800 ? ?) + k.360, med k? B
Obs: x är i grader
Om sin x = sin A (x? R), då:
x = A + k.2? eller x = (? A) + k.2?, med k? B
Obs: x är i radianer
3. Trigonometri vinkelmängd och skillnad
Den tredje formeln i trigonometri är formeln för summan och skillnaderna i trigonometriska vinklar. Formeln är:

Denna formel används för att lägga till vinklar och sidor i en triangel.
4. Formel för multiplikation av trigonometri

När det gäller multiplikationen i triangelns vinklar och sidor kan du använda den trigonometriska multiplikationsformeln ovan.
5. Formler för trigonometri Belopp och skillnad

I triangeln finns det inte bara tillsatsformeln utan det finns också en sida som måste summeras samtidigt som letar efter skillnaden med formeln för summan och den trigonometriska skillnaden ovan.
6. Trigonometri-dubbla och tre vinkelformler

7. Trigonometry Half Angle Formula

Vinklar som kan beräknas på en triangel är inte bara fulla vinklar utan halva vinklar av en triangel kan beräknas med formeln för de trigonometriska halvvinklarna ovan.
8. Trigonometri specialvinkelformler

Förutom de sju formlerna ovan finns det också speciella vinklar i den trigonometriska formeln

Så när du arbetar med ett problemtrigonometri måste du ta reda på i förväg om problemet är ett problem med den vanliga trigonometri formeln eller med en speciell trigonometrisk problemformel. Eftersom varje formel du använder ger olika resultat såväl som noggrannhet i att svara på frågor.
Exempel på trigonometri
Hur? Förstår du om den trigonometriska formeln ovan? Faktum är att formeln är ganska svår att förstå, men det betyder inte att du inte kan göra det om du fortsätter att försöka. Du kan också förstå trigonometriska formler genom trigonometriska problem. Som för några exempel på frågor om trigonometri som du kan prova är:
1. Bestäm värdet på sin 105º + sin 15º
Det trigonometriska problemet ovan är ett trigonometriproblem av adypstyp så att du kan använda den trigonometriska formeln för tillägg som är 2 sin ½ (A + B) cos ½ (A-B). Processen är:
värdet på sin 105 ° + sin 15 ° = 2 sin ½ (105 + 15) ° cos ½ (105-15) °
= 2 sin ½ (102) ° cos ½ (90) °
= sin 60 ° cos 45 °
Så svaret på problemet sin 105º + sin 15º är sin 60º cos 45º.
2. Hitta ekvationsvärdet för sin xº sin 25º
Lösa problemen ovan, nämligen:
x = 250 + k.3600 eller x = (1800 ? 250) + k.3600
= 1550 + k.3600
Så, x = 250 + k.3600 eller 155º + k.3600
Så ekvationsvärdet för sin xº sin 25º är x = 250 + k.3600 eller 155º + k.3600.
3. Bestäm värdet för multiplikation 2 cos 75º cos 15º
Det tredje problemet ligger ovanför den trigonometriska multiplikationsmodellen. Formeln som används är 2 cos A cos B = cos (A + B) + cos (A-B). Lösningen på problemet är:
2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75 - 15) °
= cos 90 ° + cos 60 °
= 0 + ½
= ½
Så resultatet av att multiplicera 2 cos 75º cos 15º är ½.
4. a triangel ABC skarp punkt, känd cos A = 4/5 och sin B = 12/13, då är sin C ...
Eftersom triangeln ABC har en skarp vinkel, är vinklarna A, B och C också akuta, så:
cos A = 4/5, sedan synd A = 3/5,
sin B = 12/13, sedan cos B = 5/13
A + B + C = 180 °, (antal vinklar i en triangel = 180)
A + B = 180 - C
sin (A + B) = sin (180 - C)
synd A. cos B + cos A. syn B = sin C, (vinklar på sammanhängande trianglar: sin (180-x) = sin x)
sin C = sin A.cos B + cos A.sin B
sin C = 3 / 5,5 / 13 + 4 / 5,12 / 13
sin C = 15/65 + 48/65 = 63/65
Från formeln ovan är sin C-värdet 63/65
5. Bestäm värdet på synd 120O
För fråga nummer 5 finns det två sätt att lösa det. Det första sättet är:
120 = 90 + 30
Så synd 120O kan beräknas med formeln Sin 120O = Sin (90O + 30O) = Cos 30O (erhöll ett positivt värde eftersom 120º är i kvadrant II (2), så resultatet är också positivt)
Cos 30O = ½ √3
Eller på det andra sättet, nämligen:
Samma som 180O-80°
Synd 120O = Sin (180O - 60O) = sin 60O = ½ √3
Så resultatet av sin 120º är ½ √3.
6. a ABC-triangeln har sidolängd AB = 6 cm, BC = 8 cm AC = 7 cm. Värdet på cos A är ..
Hur man gör problemet ovan är med formeln:
Cos A = (AB² + AC²-BC²) / 2 (AB. AC)
Cos A = 6² + 7²-8² / 2 (6. 7)
Cos A = 36 + 49-64 / 2 (42)
Cos A = 21/84
Så att cos A befanns vara 21/84.
7. Punkterna P och Q uttrycks med polära koordinater. Bestäm sedan avståndet mellan punkterna P och Q!

För problemet ovan använder du konsinusformeln, som är:
POQ-vinkelens storlek = 180O - (75O45O) = 60O.
PQ2 = OQ2 + OP2 - 2.OQ.OP cos ∠POQ
PQ2 = 32 + 52 - 2.3.5 cos 60O c
PQ2 = 9 + 25 - 30. 0,5
PQ2 = 9 + 25 -15
PQ2 = 19
PQ = √19 = 4,36
Då är avståndet mellan P och Q 4,36.
Nu var det en del diskussioner om trigonometriska formler och exempel på problemet. Hoppas att det är användbart för dig.








