Formel för byggnadsutrymme och exempel på frågor och diskussioner

Du måste ha hört ordet vakna oftautrymme medan du studerar matematik i skolan. Typer av olika typer av byggnader. Byggnadsutrymme kan tolkas som ett objekt eller ett rum med en tredimensionell form som har både innehåll och volym och har gränser (sidor).

Tja, bygga exempel runag är kuber, balkar, triangulära prismor, rektangulär pyramid, triangulär pyramid, kottar, rör och sfärer.

Varje byggnad har en yta och en boll. För att bättre förstå formeln som används för att hitta den, gå vidare lyssnade på en förklaring av formeln för byggnadsutrymme och exempel på problemet nedan:

Space Build Formula

1. Kuben

Vad är en kub? Kuben är en bygga utrymme the platt sida, var alla revben har samma längd liksom alla sidor av en kvadratisk form. Till exempel tärningar, rubik, kartong och andra.

Innan du diskuterar runagformeln, först veta, vad är kubens natur? Tja, här är kubens natur:

Sikt kubens egenskaper:

• Alla sidor av kuben är rektangulära
• Har 8 hörn
• Har 12 revben av samma längd
• Den har 12 diagonala plan (siddiagonaler) av samma längd
• Har 4 diagonaler av samma längd
• Har 6 sidostycken
• Har 6 rektangulära diagonala fält

Eftersom kuben är en byggnad, finns det naturligtvis sakervi måste beräkna, som volym eller ytarea. Här är några formler som du kan använda för att lösa problem i en kub:

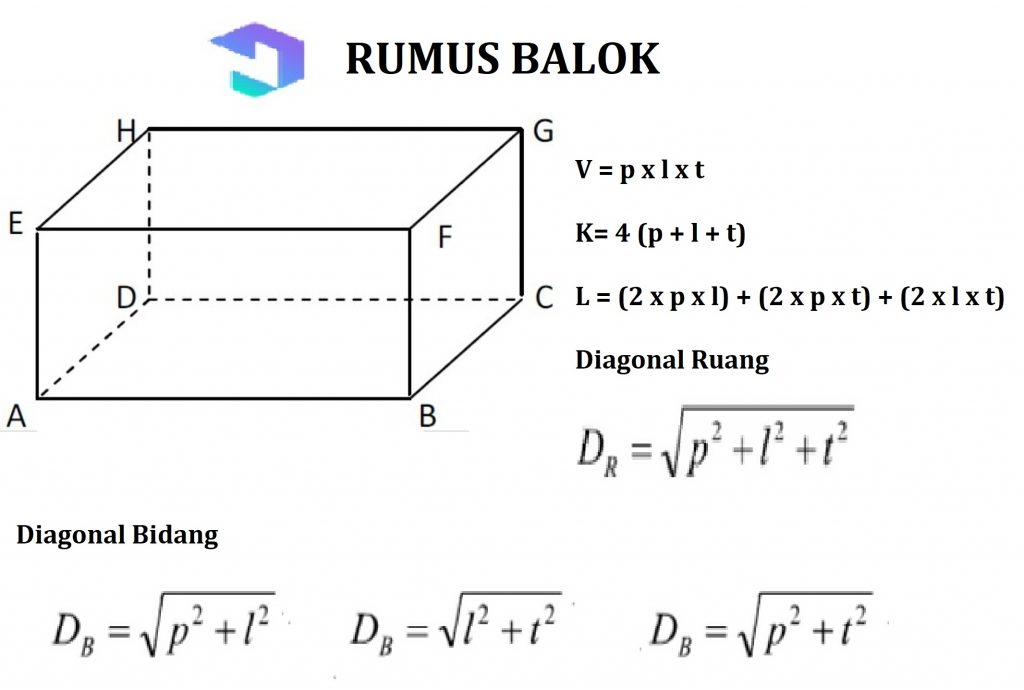
2. Strålar

Bygg ett plant sido rum den andra är strålen, med 3 par sidor med storlek och form liksom möta varandra, Rektangulär sidoform.

Strålens egenskaper:

• Att ha en sida med en lång persengi-form
• Har ribbor parallella med samma storlek
• Ha diagonaler mot varandra och i samma längd
• Har diagonalt utrymme i samma längd

3. Triangulära prismer

prisma är bygga utrymme vem har piedestal fält och övre fältet the kongruent och parallell, Anledningen till att det är kongruent och lika, Ja eftersom den andra sidan av prismat är upprätt och formen är jajargenjang eller rektangulär. Congruent är kongruent och lika.

Det finns flera typer av prismor som det femkantiga prisma, fyrkantiga prisma och triangulära prisma. Det som skiljer det är antalet former av bas och tak den har.

Egenskaperna hos ett triangulärt prisma:

• Den har 3 sammanhängande tak och basar.
• Varje sida av sidan som en stege och rektangulär
• I allmänhet har upprättstående revben (vissa är inte upprätt)
• Varje diagonalt plan på samma sida har samma storlek

Följande formler används vanligtvis för att hitta ytarea, volym av triangulära prismor:

4. Fyrsidiga limas

Fyrkantig pyramid är en bygga utrymme vem har rektangulär form. Vanligtvis har pyramiden ett sidoplan som är upprätt och triangulärt och vilar på en punkt eftersom den korsar varandra.

Följande är formler som kan användas i en fyrkantig pyramid:

5. Triangulära limas

Triangulära limas är en bygga utrymme vem har triangulär bas. Vanligtvis har pyramiden ett upprätt sidoplanoch har triangulär form och vilar på en punkt eftersom de korsar varandra. Det som skiljer namnet på pyramiden är formen på basen som den täcker, såsom pentagonpyramiden, den fyrkantiga pyramiden och den triangulära pyramiden.

Följande är formler som kan användas i en pyramid:

6. Kottar

En kon är ett rum med en formad bascirkeln och har ett sidoplanfilt och är bildat av en cirkel som en kil. Du måste ofta se födelsedag hattar eller keps hattar för bönder. Tja, det är ett exempel på en konform.

Egenskaper hos kottar:

• Har två revben
• Att ha ett toppunkt som ett toppmöte
• Har 2 sidplan (cirkelns sidor består av ett och som bas- och ett filtfält)

Följande är formler som kan användas för att lösa problem i konisk rymdkonstruktion:

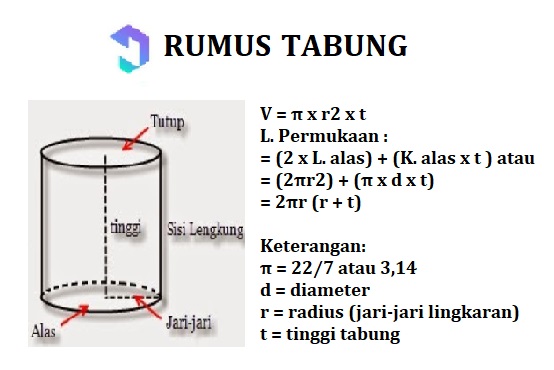
7. Tube

Röret är en bygga utrymme bestående av bas och lock i formen cirkeln, liksom att ha krökt filt, från sidan en rektangel.

Rörets egenskaper:

• Ha en matta och lock i samma storlek
• Har två revben
• Har 3 fält (2 cirklar och 1 rektangel)
• Har inte ett toppunkt

Allmän formel för beräkning av rörets volym och volym:

8. Boll

Vi ser ofta bollen i vardagen, till och med några av er gillar riktigt bollspel. Japp, bollen är en som vaknar utrymmehar ytarea och även volym. Detta hänför sig också till varför bollen enkelt kan driblas och kontrolleras eftersom de två sakerna är svaret.

Bollegenskaper:

• Den har inga toppar och revben
• Har samma avstånd till centrum vid kurvpunkten.

Följande är en formel för att hitta volym och ytarea för en sfär:

Exempel Frågor + Diskussionen

1. En rubik har en sidolängd på 5 cm. Vad är volymen på rubiken?

Svar:

V = s x s x s

= 5 x 5 x 5

= 125

Så volymen på rubiken 125 cm³

2. Ett block har en längd på 8 cm, bredden 5 cm och höjden 4 cm. Vad är blockets omkrets?

K = 4 (p x l x t)

= 4 (8 x 5 x 4)

= 640

Så strålens omkrets är 640 cm

3. Ta reda på vad volymen på det triangulära prismen är om basytan är 16 cm och höjden är 10 cm!

Svar:

V = L-bas x t

= 16 x 10

= 160

Så volymen 160 cm²

4. Beräkna volymen för den rektangulära pyramiden om den är 6 cm lång, 4 cm bred och 9 cm hög

Svar:

V = 1/3 (p x l x t)

= 1/3 (6 x 4 x 9)

= 71

Så den rektangulära pyramidvolymen är 72 cm²

5. Beräkna volymen för triangelpyramiden om basområdet är 24 cm och höjden är 5 cm?

Svar:

V = 1/3 (L-bas x t)

= 1/3 (24 x 5)

= 40

Så ytytan är 40 cm²

6. En födelsedags hatt har en radie på 7 cm, vad är basen på hatten?

Svar:

L-bas = πr²

= 7/22 x 7²

= 154

Så bred bas födelsedag hatt är 154 cm

7. Rörets radie är 15 cm. Om höjden är 20 cm är rörets volym ...

Svar:

V = πr²t

= 3,14 x 15² x 20

= 14,130

Så rörets volym är 14,130 cm²

8. Cykelhjulet har en radie på 14 cm. Bestäm ytan på cykelhjulet!

Svar:

L = 4πr²

= 4 x 22/7 x 14²

= 2464

Så ytytan på cykelhjulen vars ekrar är 14 cm är 2464 cm²

Det är diskussionen om formeln för byggnadsutrymme (ytor och volym för varje byggnadsutrymme) komplett med provproblem och diskussioner. Förhoppningsvis användbar och lätt att förstå!