Soru Örnekleriyle Aritmetik ve Geometri Formülleri ve Tartışılması
Bu makalede aritmetik ve geometrik formüller, soru örnekleri ve bunların tartışılması tartışılacaktır.
Aritmetik ve geometri konularımızdırmatematikte okulda öğrenir. Ulusal sınavlar, kolej giriş sınavları veya iş başvurularında yapılan sınavların her ikisi hakkında sık sık sorular olduğu durumlarda.
Sadece bu değil, aynı zamandaAritmetik sekanslar ve satırlar veya geometrik sekanslar ve satırlar arasında, çünkü sekansların ve satırların kuralları, banka faizi, üretim artışları ve bir işletme için kar / zarar gibi hesaplamaları tamamlamamıza yardımcı olabilir. Tamam, aşağıdaki açıklamaya bakalım!
Aritmetik Formüller
-
Aritmetik Sıra

Yukarıdaki tabloya bakın, soldan sağa doğru sayılardaki farkın nasıl olduğunu gözlemleyin? Ve sonra, yukarıdan aşağıya sayılardaki farkı gözlemleyin?
Gözlemlerden, bir çizgiden farkın her zaman sabit olduğunu görüyoruz. Örneğin sağ sıramızdan sola doğru: 1, 2, 3, 4, 5 (fark 1'dir).
5 - 1 = 4; 4 - 1 = 3; 3 - 1 = 2; 2-1 = 1
Ve yukarıdan aşağıya: 1, 6, 11, 16 (fark 5).
16-5 = 11; 11-5 = 6; 6-5 = 1
Bunun gibi satırlara aritmetik diziler denir.
Sabit bir değere sahip olan fark denir fark ve tarafından sembolize edilir b. Genel olarak, Un hece formülüdürn bir aritmetik dizi
b = Un - UN-1
İlk dönem (u1) tarafından sembolize edildi bir ve fark şu şekilde sembolize edilir: b, daha sonra formül terimin dizi aşağıdaki gibi türetilebilir.
U1= a
U2= U1 + b = a + b
U3= U2 + b = (a + b) + b = a + 2b
U4= U3 + b = (a + 2b) + b = a + 3b
U5= U4 + b = (a + 3b) + b = a + 4b
Böylece, terimler şu şekilde formüle edilebilir:n aritmetik sıralaması
Un= a + (n - 1)b
Açıklamalar:
Un= kabilen
a = ilk hece
b = fark
n = birçok kabileler
-
Aritmetik Serisi
Aritmetik dizi terimleri birlikte eklenirse, bir aritmetik dizi elde edilir. Örneğin U1, U2, U3, ……., Un o zaman aritmetik rütbeleri U1 + U2 + U3 + .... + Un denilen aritmetik ilerleme. Aritmetik seriler n S gösterimi ile yazılmışn ile Un= a + (n - 1)b.
Yani, aritmetik ilerleme için genel formül
Sn= 1/2 n (a + Un)
Sn= 1/2 n (2a + (n - 1) b)
Açıklamalar:
Sn= aritmetik ilerleme sayısı
a = ilk hece
b = fark
Un= kabilen
n = birçok kabileler
Terimi belirlemekn sayı formülü biliniyorsa aritmetik dizi n ilk kabile. Kabilen aşağıdaki formül ile belirlenebilir.
Un = Sn - SN-1
-
Arisan soy veya Aritmetik Orta Kabile
Aşağıdaki aritmetik diziyi biliyorsanız: U1, U2, U3, ……., Un birçok aritmetik yürüyüş kabilesi iletuhaf, bu yüzden çizginin ortasında çizgiyi 2 eşit parçaya bölen bir terim var. Diyelim ki dizinin orta terimi Ut, Yani orta terimi bulmak aşağıdaki gibidir.

Açıklamalar:
Ut= aritmetik rütbelerinin orta kabilesi
a = ilk hece
Un= aritmetik sıralamalarının son kabilesi n garip
-
Aritmetik Satıra Ekle
Örneğin U1, U2, U3, ……., Un başlangıç hecesi olan aritmetik bir dizidir U1. İki ardışık terim arasına sokulmuşsa k yeni aritmetik sekanslar oluşacak şekilde sayılar, farklı yeni aritmetik sekanslar aşağıdaki gibi oluşturulur.
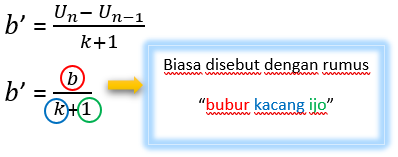
Açıklamalar:
b ’= eklemeden sonra yeni fark
b = eklemeden önce farklı
k = eklenen numara
Geometri Formülleri
-
Geometri Çizgisi
1, 2, 4, 8, 16, satırlarını gözlemlemeye çalışın. Bir sonraki terimin, önceki terimde 2 ile çarpılmasıyla elde edildiğine bakın. Bu dizi geometrik diziyi içerir.
Yani, genel olarak sonuçlandırılabilir, geometrik dizi "Halojen" terimi, bir önceki terimden elde edilen her kabilenin sabit bir sayıyla (sabit) çarpılmasıyla bir sayı dizisidir. Bu sabit numaralar denir oranı (karşılaştırma) ve simgeleyen r.
eğer U1, U2, U3, U4......., Un geometrik sıra ile Un formülün ve oran r, geçerlidir:
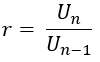
Kabile için genel formüln birinci terimli geometrik dizi (U1) beyan edildi bir ve oran r, aşağıdaki gibi türetilebilir.
U1= a
U2= U1 x r = ar
U3= U2 x r = ar²
U4= U3 x r = ar3
::
Un= UN-1 x r = arN-2 x r = arN-1
Böylece geometrik dizi elde edildi a, ar, ar², ...., arN-1.
Yani, genel formüln geometrik dizi
Un= arN-1
Açıklamalar:
Un = kabilen
a = ilk hece
r = oran
n = birçok kabileler
-
Geometri Serisi
eğer U1, U2, U3, U4......., Un o zaman bir geometri sırasıdır U1 + U2 + U3 + U4 + …… .. Un bir geometri serisi ile Un = arN-1.
Miktarları belirlemek için genel formül n geometrik dizinin ilk terimi aşağıdaki gibi türetilebilir.
Örneğin Sn miktarların gösterimi n ilk hece.
Sn = U1 + U2 + U3 + …… .. Un
Sn = bir + ar + ar2 + ... .. + arN-1...........................................................................(1)
Her iki segment de çarpılırsa r, sonra
rSn = ar + ar2 + ar3 + ... .. + arn........................................................................(2)
(1) ve (2) denklemlerindeki farktan,

Yani, toplam formül n geometri serisinin ilk terimi aşağıdaki gibidir.

Açıklamalar:
Sn = miktar n ilk hece
a = ilk hece
r = oran
n = birçok kabileler
-
Çizginin Merkez Kabilesi veya Geometri Serisi
Örneğin, aşağıdaki geometri çizgisini bilin: U1, U2, U3, U4......., Un (terim sayısı gariptir). Çizginin orta terimi Ut, o zaman formül aşağıdaki gibidir.
Açıklamalar:
Ut= orta vadeli geometrik dizi
a = ilk hece
Un= sayıyla son dönem geometrik sırası n garip
-
Geometri Satırına Ekle
Geometri satırına yerleştirilirse k sayılar iki ardışık terim arasında öyle bir şekilde olur, böylece yeni geometrik çizgiler oluşur. Böylece yeni oranı bulmak için aşağıdaki gibi formüle edilebilir.

Açıklamalar:
r ’= yerleştirmeden sonra yeni oran
r = yerleştirme öncesi oran
k = eklenen numara

-
Sınırsız Geometri Serisi
Sonsuz bir geometri serisi, kabilelerinin çoğu tarafından kesilemeyen geometrik bir seridir. Aşağıdaki örneği düşünün!
a. 1 + 2 + 4 + 8 + ...
b. 5-10 + 20-40 + ...
c. 1 + 1/2 + 1/4 + 1/8 + ...
d. 9-3 + 1 - 1/3 + ...
Yukarıdaki seri, sonsuz bir geometri serisinin bir örneğidir. A ve b örneklerini ele alalım. Dizi ıraksak seriler, yani belirli bir değere gitmeyen ve oranı olan bir seri r ile | r | > 1.
Daha sonra, c ve d örnekleri yakınsak seriler, yani belirli bir değere giden ve oranı olan bir seri r ile | r | <1.
Yakınsama serilerinde, terimlerin sayısı belirli bir fiyatı aşmayacak, ancak belirli bir fiyata yaklaşacaktır. Bu belirli fiyata denir sonsuz terim sayısı S ile gösterilen∞. S değeri∞ tüm terimin (S) yaklaşım değerini (limit) temsil edern) ile n sonsuzluğa yaklaşıyor. Bu nedenle sonsuz seri formül, ilk terimle geometrik seriden türetilebilir a, ve n → ∞.

Çünkü seri yakınsama (| r | <1), için n → ∞, sonra arn→ 0 böylece

Sonsuz geometrik dizi sayısının formülü,
Örnek Sorular ve Tartışma
1. -3, 2, 7, 12, ... satırlarının 6. ve 10. terimlerini belirleyin.
tartışma:
bir = -3
b = Un - uN-1 = 2 - (-3) = 5
Un = a + (n-1) b, o zaman:
U6 = (-3) + (6-1) 5 = 22
U10 = (-3) + (10-1) 5 = 42
2. 2 + 4 + 6 + 8 + serisinin ilk 90 terimini bulun
tartışma:
bir = 2
b = 4-2 = 2
n = 90
sonra,
Sn= 1/2n (2bir + (N-1)b)
Sn= 1/2 x 90 (2 (2) + (90-1) 2)
Sn= 45 (4 + 178)
Sn= 45 (182)
Sn= 8.190
Bu nedenle, serinin ilk 90 terimi 8.190'dır.
3. Aritmetik dizi 3, 5, 7, 9, .... 1.007 bilinmektedir.
Çizginin orta terimini belirleyin.
tartışma:
a = 3
b = 5-7 = 2
Un = 1.007, sonra:
Ut = 1/2 (bir + Un)
Ut = 1/2 (3 + 1.007)
Ut = 1/2 (1.010)
Ut = 505
4. Bilinen satırlar 2, 12, 22, 32, .... İki ardışık terim arasında, 4 sayı yeni bir aritmetik dizi oluşturulacak şekilde eklenir. belirleyin:
a. Yeni bir fark
b. N. terim formülü
c. Yeni aritmetik dizinin ilk n terimi.
tartışma:
a.

b. N. Terim formülü,
Un = a + (n-1) b
Un = 2 + (n-1) 2
Un = 2 + (2-n-2)
Un = 2n
c. İlk terimin n sayısı
Sn= 1/2n (bir + Un )
Sn= 1/2n (2 + 2n)
Sn= n (n + 1)
5. Geometri sırasının 2, 6, 18, 54, ilk terimini, oranını ve 8. terimini arayın ...
tartışma:
a = 2
r = U2/ U1 = 6/2 = 3
sonra,
Un= arN-1
U8= ar8-1
U8= 2 (38-1)
U8= 2 (37)
U8= 2 (2.187)
U8= 4.374
6. 2 + 4 + 8 + 16 + geometri serisi sayısını belirleyin ... (8 kabileler)
tartışma:
bir = 2
r = U2/ U1 = 4/2 = 2 (r> 1)
İlk 8 terime kadar olan seri sayısı, n = 8

Yani, geometrik dizinin ilk 8 terimi 510'dur.
7. Geometri sıraları 1/8, 1/4, 1/2, 1, 2, 4, .... 2048 olarak bilinir. Çizginin orta terimini belirleyin.
tartışma:
a = 1/8
r = U2/ U1 = 1/8: 1/4 = 2
Un = 2.048
sonra,
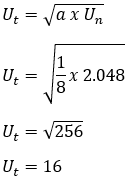
8. Geometrik sekansın 1/32, 1/16, 1/8, 1/4, .... olduğu bilinmektedir. İki ardışık terim arasında, üç sayı yeni bir geometrik sekans oluşturulacak şekilde eklenir. belirleyin:
a. Yeni geometri çizgilerinin pozitif oranı
b. Yeni geometri dizisinin n. Terim formülü
c. Yeni geometri satırının ilk n terimi.
tartışma:
Geometri sırası 1/32, 1/16, 1/8, 1/4, ... veya ayrıca servis edilebilir 2-5, 2 -4, 2-3, 2-2, ....
a. Ardışık iki terimi düşünün, örneğin U1 ve sen2 = 1/32 ve 1/16, o zaman:

b. N. Terim formülü,
Un= arN-1
Un= 2-5(2n / 4-1)
Un= 2n / 4-6
c. Toplam n ilk dönem

9. 1 + 1/2 + 1/4 + 1/8 + geometrik serilerin sonsuz sayıda terimini belirleyin ...
tartışma:
a = 1
r = U2/ U1 = 1/2: 1 = 1/2
sonra,

10. Bir geometri serisinin ilk terimi 2 ve sonsuzdan toplama 4'tür. Oranı bulun.
tartışma:
a = 2
S∞ = 4
o zaman S formülünü değiştiririz∞
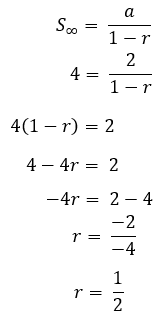
Soru ve tartışma örnekleri ile birlikte aritmetik ve geometri formüllerinin açıklamasıdır. Faydalı olabilir !








