Bina Alanı Formülü ve soru-tartışma örnekleri

Kelimenin sık sık uyandığını duymuş olmalısınızmatematik okurken boş alan. Çeşitli bina türleri. Bina alanı, hem içeriği hem de hacmi olan ve sınırları (kenarları) olan üç boyutlu bir şekle sahip bir nesne veya oda olarak yorumlanabilir.

Eh, yapı örneği runag küpler, kirişler, üçgen prizmalar, dikdörtgen piramit, üçgen piramit, koniler, tüpler ve toplar.

Her binanın yüzey alanı ve topu vardır. Bulmak için kullanılan formülü daha iyi anlamak için, devam et bina alanı için formülün bir açıklamasını ve aşağıdaki problem örneklerini dinledi:

Uzay Oluşturma Formülü

1. Küp

Küp nedir? Küp bir alan inşa et the düz taraf, nerede tüm kaburgalar aynı uzunluktadır yanı sıra kare şeklinin her tarafı. Örneğin zar, rubik, karton ve diğerleri.

Runag formülünü tartışmadan önce, bil, küpün doğası nedir? İşte küpün doğası:

Küpün eleme özellikleri:

• Küpün her tarafı dikdörtgen şeklindedir
• 8 köşesi vardır
• Aynı uzunlukta 12 kaburga vardır
• Aynı uzunlukta 12 diyagonal düzlem (yan köşegen) vardır
• Aynı uzunlukta 4 köşegen vardır
• 6 yan parçası vardır
• 6 adet dikdörtgen diyagonal alana sahiptir

Küp bir yapı alanı olduğu için, elbette bir şeyler varhacim veya yüzey alanı gibi hesaplamamız gerekir. Küp içindeki sorunları çözmek için kullanabileceğiniz bazı formüller:

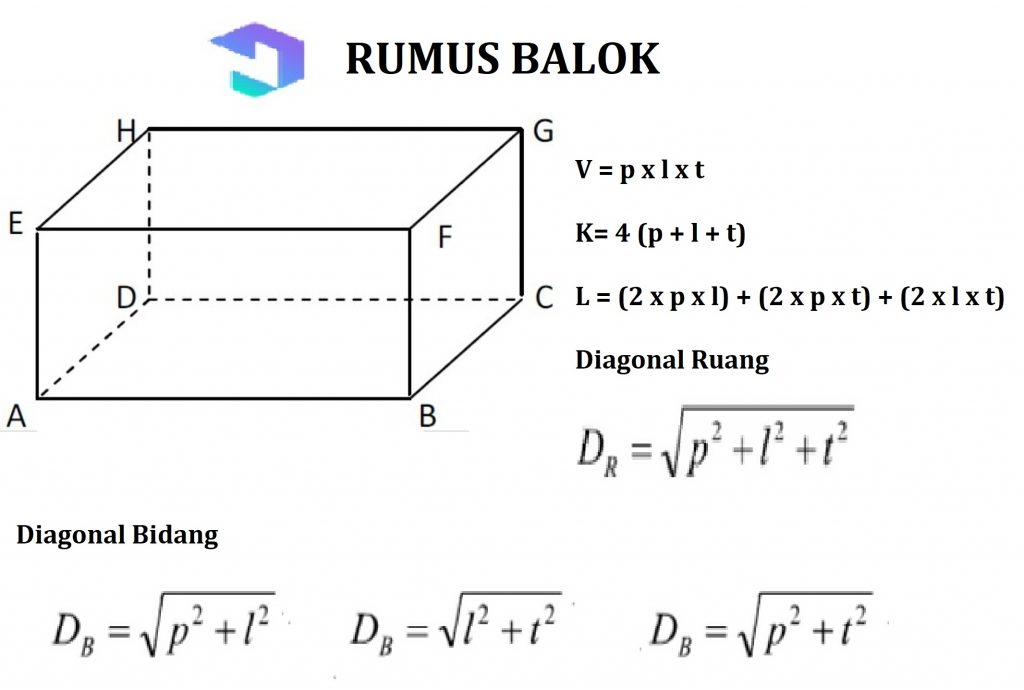
2. Kirişler

Düz yan oda inşa et ikincisi ışın Boyut ve şekil ile 3 çift kenar yanı sıra yüzleşmek, Dikdörtgen yan şekil.

Kirişin özellikleri:

• Uzun persengi şeklinde bir tarafa sahip olmak
• Aynı boyuta paralel kaburgalara sahip olmak
• Çaprazlamaların birbirine bakacak ve aynı uzunlukta olması
• Aynı uzunluktaki diyagonal alana sahiptir

3. Üçgen Prizmalar

prizma olduğu alan inşa et kim var kaide alanı ve üst alan the uyumlu ve paralel, Eşit ve eşit olmasının nedeni, evet çünkü prizmanın diğer tarafı diktir ve şekil jajargenjang veya dikdörtgen şeklindedir. Eşlik uyumlu ve eşittir.

Beşgen prizma, dörtgen prizma ve üçgen prizma gibi çeşitli prizmalar vardır. Onu ayıran şey, sahip olduğu taban ve çatı formlarının sayısıdır.

Üçgen prizmanın özellikleri:

• 3 adet uyumlu çatı ve tabana sahiptir.
• Tarafın her tarafı merdiven merdiveni gibi ve dikdörtgen
• Genellikle dik kaburgalar vardır (bazıları dik değildir)
• Aynı taraftaki her çapraz düzlem aynı boyuta sahiptir

Aşağıdaki formüller yüzey alanını, üçgen prizmaların hacmini bulmak için yaygın olarak kullanılır:

4. Dörtlü Limanlar

Dörtgen piramit bir alan inşa et kim var dikdörtgen şekilli taban. Genellikle piramidin dik ve üçgen şeklinde bir yan düzlemi vardır ve kesiştiği için bir noktada durur.

Dörtlü bir piramitte kullanılabilen formüller şunlardır:

5. Üçgen Limanlar

Üçgen limanlar bir alan inşa et kim var üçgen taban. Genellikle piramidin dik bir yan düzlemi vardırve üçgen şeklindedir ve kesiştikleri için bir noktada dinlenirler. Piramidin adını ayıran şey, pentagon piramidi, dörtgen piramit ve üçgen piramit gibi kapsadığı tabanın şeklidir.

Aşağıdakiler bir piramitte kullanılabilen formüllerdir:

6. Koniler

Bir koni şekilli tabanı olan bir odadırdaire ve bir yan düzlem battaniye vardır ve bir kama gibi bir daire oluşur. Çiftçiler için genellikle doğum günü şapkaları veya şapka şapkaları görmelisiniz. Eh, koni şekline bir örnektir.

Konilerin özellikleri:

• 2 kaburga var
• Tepe noktası toplantısı olarak tepe noktasına sahip olmak
• 2 yan düzlemi vardır (dairenin kenarları bir, taban ve bir battaniye alanından oluşur)

Konik alan yapımında problem çözmede kullanılabilecek formüller şunlardır:

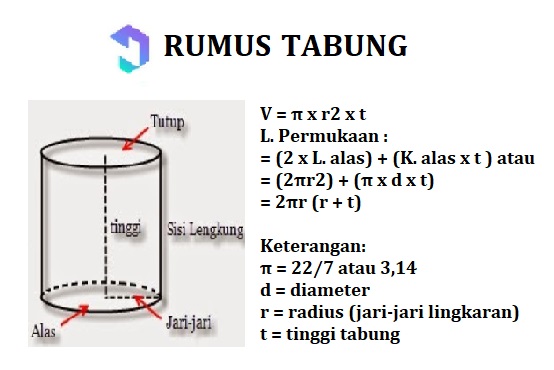
7. Tüp

Tüp bir alan inşa et oluşan kaide ve bu şekli örtün daireyanı sıra kavisli battaniye, yandan Bir dikdörtgen.

Tüp özellikleri:

• Aynı boyutta bir tabana ve kapağa sahip olun
• 2 kaburga var
• 3 alanı vardır (2 daire ve 1 dikdörtgen)
• Tepe noktası yok

Tüplerin alan ve hacmini hesaplamak için genel formül:

8. Top

Topu günlük hayatta çok sık görüyoruz, bazılarınız bile top oyunlarını çok seviyor. , yep top alanı uyandırıyoryüzey alanı ve ayrıca hacim var. Bu aynı zamanda topun neden kolayca toplanıp kontrol edilebildiği ile de ilgilidir, çünkü iki şey cevaptır.

Top özellikleri:

• Köşeleri ve kaburgaları yoktur
• Eğri noktasında merkeze aynı mesafeye sahip olun.

Aşağıdakiler bir kürenin hacmini ve yüzey alanını bulmak için bir formüldür:

Örnek Sorular + Tartışma

1. Rubik kenar uzunluğu 5 cm'dir. Rubik hacmi nedir?

Cevap:

V = s x s x s

= 5 x 5 x 5

= 125

Yani rubik hacmi 125 cm³

2. Bir bloğun uzunluğu 8 cm, genişliği 5 cm ve yüksekliği 4 cm'dir. Bloğun çevresi nedir?

K = 4 (p x l x t)

= 4 (8 x 5 x 4)

= 640

Kirişin çevresi 640 cm

3. Taban alanı 16 cm ve yükseklik 10 cm ise üçgen prizma hacminin ne olduğunu öğrenin!

Cevap:

V = L taban x t

= 16 x 10

= 160

Yani hacim 160 cm²

4. 6 cm uzunluğunda, 4 cm genişliğinde ve 9 cm yüksekliğinde dikdörtgen piramidin hacmini hesaplayın

Cevap:

V = 1/3 (p x l x t)

= 1/3 (6 x 4 x 9)

= 71

Yani dikdörtgen piramit hacmi 72 santimetre²

5. Taban alanı 24 cm ve yüksekliği 5 cm ise üçgen piramidin hacmini hesaplayın?

Cevap:

V = 1/3 (U taban x t)

= 1/3 (24 x 5)

= 40

Yani yüzey alanı 40 santimetre²

6. Doğum günü şapkası yarıçapı 7 cm, şapka tabanı nedir?

Cevap:

L tabanı = πr²

= 7/22 x 7²

= 154

Yani geniş tabanlı doğum günü şapkası 154 cm

7. Bir tüpün yarıçapı 15 cm'dir. Yükseklik 20 cm ise, tüpün hacmi ...

Cevap:

V = πr²t

= 3,14 x 15² x 20

= 14.130

Böylece tüpün hacmi 14.130 cm (santimetre)²

8. Bisiklet tekerleğinin yarıçapı 14 cm'dir. Bisiklet tekerleğinin yüzey alanını belirleyin!

Cevap:

L = 4πr²

= 4 x 22/7 x 14²

= 2464

Konuşmacıları 14 cm olan bisiklet tekerleklerinin yüzey alanı 2464 cm (santimetre)²

Bu, örnek problemler ve tartışma ile birlikte bina alanı formülü (her bir bina alanının yüzey alanı ve hacmi) hakkındaki tartışmadır. Umarım faydalı ve kolay anlaşılır!