Leren van Pascal Law: formules, geluiden, voorbeelden van vragen en hun discussie

De naam van de wet van Pascal komt van mensendie een experiment had uitgevoerd, de naam van de wetenschapper was Blaise Pascal. Hij heeft experimenten met water uitgevoerd en hij heeft ook verklaard dat water verder en zwaarder naar buiten kan komen door door een gat in de container te gaan waar het bovenoppervlak open is.

En in vergelijking met containers die oppervlak zijnde bovenkant is gesloten, het wordt ook vaak aangeduid met de naam van het pascal-principe. En dit wordt ook veroorzaakt door een hogere waterdruk op de open container.

Met bovenstaande uitleg kan ade vraag is, waarom kan de waterdruk op een blootgesteld containeroppervlak groter zijn dan die van een gesloten container?

Dat komt omdat de gesloten container alleen waterdruk heeft die afhankelijk is van de dichtheid van water, de diepte van het water door de versnelling van de zwaartekracht en het oppervlak.

Vergeleken met open wada,afgezien van wat er in een gesloten container zit, is er ook luchtdruk die op een wateroppervlak heeft gewerkt, en dat is de reden.

Geluiden van de wet van Pascal

Geluid en formule voor de wet van Pascal

Voordat je weet wat het geluid van de wet van Pascal is,U moet van tevoren weten wat het begrip van de wet van Pascal is. De wet van Pascal is een toepassing van een concept van druk in een vloeistof.

Een eenvoudig voorbeeld van de wet van Pascal is, alsJe hebt een monteur een band zien verwisselen, er is zeker een auto aangesteld met speciaal gereedschap. Nu wordt een gereedschap dat de auto kan heffen ook wel een krik genoemd.

Nou, het principe van krikwerk kun je ook leren van de wet van Pascal. Het geluid van de wet van Pascal is ook opgenomen in het principe van de wet van Pascal. Het volgende klinkt de wet van Pascal:

De wetformule van Pascal

Net als bij andere natuurkundige wetten heeft ook de wet van Pascal een formule. Waar de formule een referentie wordt bij het werken aan problemen met de wet van Pascal.

Simpel gezegd, het volgende is de juridische formule van Pascal op een gesloten systeem:

Eenvoudigere vormen van formules kunnen daar ook op geschreven worden P.₁= P_2.

Zoals we allemaal wetendat de druk een kracht is die wordt gedeeld door de omvang van het uiterlijk of kan worden geschreven met P = F / A, daarom kan de vergelijking als volgt worden herschreven:

En als wat bekend is de diameter of straal is, dan kan de formule van de wet van Pascal ook veranderen en als volgt worden:

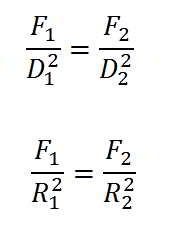
Ket:

F1 = kracht op doorsnede 1 (newton)
F2 = kracht op sectie 2 (newton)
A1 = doorsnedeoppervlak 1 (m2)
A2 = doorsnedeoppervlak 2 (m2)
D1 = diameter bij doorsnede 1 (m)
D2 = diameter bij doorsnede 2 (m)
R1 = straal van doorsnede 1 (m)
R2 = straal van doorsnede 2 (m)

Afgaande op de bovenstaande formule wordt de kracht F2 ook beïnvloed door de oppervlakte van elk oppervlak van het vaartuig. Als het oppervlak van het schip groter is, zal de gecreëerde kracht nog groter zijn.

Toepassing van Pascal Law in het dagelijks leven

De wet van Pascal kan ook voordelen opleveren inin het dagelijkse menselijke leven. Waar bij de toepassing van de wet van Pascal het dagelijkse menselijke werk kan helpen. Hier zijn enkele van de toepassingen van de wet van Pascal in het dagelijks leven:

1. Toepassing van hydraulische remmen

Wist je dat het remsysteem op eenDe auto maakt bij de fabricage vaak gebruik van de wet van Pascal? Want als je de wet van Pascal niet gebruikt, dan is er een zeer grote kracht nodig om de snelheid van een auto te kunnen stoppen.

En door deze wet te gebruiken, éénAutobestuurders leveren slechts een kleine kracht, zodat het de snelheid van een voertuig kan verminderen. Deze kracht wordt via olie via een buis doorgegeven, die later een veel grotere kracht op een rem op een autoband kan uitoefenen.

2. Toepassing van een fietspomp

Voor de toepassing van fietspompen zijn er 2 soorten fietspompen, hydraulische fietspompen en hydraulische fietspompen.

Nou, om gemakkelijker banden te kunnen pompeneen fiets dan moeten we een hydraulische fietspomp gebruiken, want het gebruik van een hydraulische fietspomp kost maar weinig energie.

3. Toepassing van hydraulische krikken

Als je ooit een monteur hebt gezienverwissel een band van een auto, dan moet een deel van de auto ergens op worden gestut zodat de carrosserie van de auto niet in een gekantelde positie staat, dus mensen gebruiken vaak een hydraulische krik.

4. Toepassing van hydraulische autoliftmachines

Bij de toepassing van de wet van Pascal ook vaakgebruikt om een auto op te tillen. En deze tool wordt vaak gebruikt in de wasstraat. Welnu, de werking van een hydraulische auto-hefmachine is ook hetzelfde als die van een hydraulische krik.

5. Toepassing van katoenpersmachine

Niet alleen remmen, pompen en krikken, toepassinguit de pascal wet bestaat ook op een katoenpersmachine. Dit is handig om een formaat te krijgen dat geschikt is voor verspreiding en ook opgeslagen.

Hoe het werkt met deze katoenen persmachinegebruikmakend van de drukkracht die wordt geproduceerd door een pomp die de kleine zuigkracht kan indrukken, die later de grote zuigkracht omhoog kan bewegen en later het katoen zal duwen, en zal maken wanneer het wordt samengedrukt.

Voorbeelden van Pascal + beantwoorden juridische vragen

Een hydraulische hendel heeft een hoofd (in) zuiger met een diameter van 1 cm en een buitencilinder met een diameter van 6 cm.

Bepaal daarom al het vermogenwordt verwijderd van de buitenste cilinder wanneer een kracht van 10 N wordt uitgeoefend op een inlaatcilinder. Als de binnenkomende zuiger binnen een afstand van 4 cm beweegt, hoe ver beweegt de buitenste zuiger dan?

Antwoord:

Het bovenstaande probleem kan worden opgelost met de volgende formule

. Maar we moeten de waarde van de geproduceerde kracht eerst vinden met behulp van de onderstaande formule:

$F_2 = (frac {A_2} {A_1}) F_1$

Uit de bovenstaande formule volgt dan de grote kracht die is gegenereerd, wat gelijk is aan:

$F_2 = frac {frac {pi} {4} (6 keer 10 ^ {- 2} m) ^ 2} {frac {pi} {4} (1 keer 10 ^ {- 2} m) ^ 2} (10 N )$ F_2 = 360 N

Vervolgens krijgen we een afstand van de beweging van een buitenste zuiger, wat gelijk is aan:

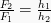
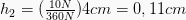
$frac {F_2} {F_1} = frac {h_1} {h_2}$ $h_2 = (frac {10 N} {360 N}) 4 cm = 0,11 cm$
Daarom kan worden geconcludeerd dat de buitenste zuiger binnen een afstand van 1/36 beweegt in vergelijking met de binnenkomende zuiger.

Dat is de discussie over de wet van Pascal, zoals formules, geluiden en voorbeelden van de wet van Pascal en haar discussie. Hopelijk nuttig en makkelijk te begrijpen. Dank je wel!

Lees meer: