GLBB- og GLB-formler med eksempler på problemer og diskusjoner

Vi er absolutt kjent med å hørestår for GLBB og GLB. Jepp! begge er materiale som vi lærer på skolen om fysikk. Hvor GLBB er Irregularly Straight Motion og GLB is Irregularly Straight Motion.

I hverdagen anvendelsen av beggevi har også opplevd at når vi sykler på en nedoverbakke, viser det seg at dette er ett eksempel på GLBB og når et tog kjører i konstant hastighet, noe som er et eksempel på GLB.

Denne artikkelen vil diskutere GLBB- og GLB-formlene komplett med prøveproblemer og diskusjon. Her er forklaringen!

Innholdsfortegnelse

GLBB-formel

Hvis det forekommer endringer i hastigheten til objekter regelmessig og den gjennomkjørte banen er en rett bane, kalles objektets bevegelse "uregelmessig endring av rett bevegelse".

Fordi endringer i hastighet som objekter oppleverordnede, med andre ord, endring i rett linje uregelmessig er bevegelse på en rett bane med konstant akselerasjon. Fra dette forholdet mellom hastighet og akselerasjon, kan vi utlede formelen for at hastigheten i rett bevegelse endres uregelmessig, som er som følger.

ved å ta t₀= 0, da:

Merknader:

v = sluttfart

v₀= begynnelseshastighet

a = akselerasjon (fast)

t = tatt tid

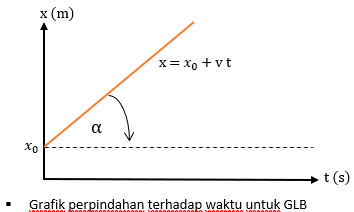
I tillegg kan vi også bestemme ligningen for forskyvning (x) rettbevegelsesendring uregelmessig basert på følgende graf.

graf v med hensyn til t i GLBB - GLBB formel

fordi v = v₀+ kl, da:

Ligninger for mer generelle tilfeller, hvor x₀ = forskyvning / startposisjon.

Så grafen for forskyvning med hensyn til tid kan beskrives som følger.

graf av x med hensyn til t i glbb - GLBB-formelen

Vel, basert på ligningen x = x₀+ v₀t + 1/2 kl² og v = v₀+ kl, kan vi bestemme forholdet mellom hastighet, akselerasjon og forskyvning for GLBB som følger.

Hvis den første overføringen, x₀= 0, da:

GLB-formel

Når et objekt går samme avstandsamtidig intervall gjennom en rett bane, kalles bevegelsen til dette objektet "uregelmessig rett bevegelse". I dette tilfellet har objektet en fast hastighet (hastighet), da er dens akselerasjon null.

På denne måten å finne avstanden, kan formuleres som følger:

s = v x t

Merknader:

s: avstand (m eller km)

v: hastighet (m / s eller km / time)

t: tid (sekund eller time)

Således er hastighetsgrafen med hensyn til bevegelsestid i form av en horisontal rett linje som det følgende.

Da kan forskyvningen formuleres med et område av ABCD, nemlig:

x = (t₁-0) x (v₀- 0)

Ved å ta karakterer t₁-0 = t og v₀- 0 = v, deretter:

x = v x t

Merknader:

x = objektbevegelse (m eller km)

v = hastighet (m / s eller km / t)

t = reisetid (andre eller time)

Fra formelen ovenfor kan vi vite at avstanden og bevegelsen til gjenstander er like i ensartet bevegelse, hvor s = v x t og x = v x t.

Mens grafen for forskyvning med hensyn til tid for denne bevegelsen hvor x₀ er startposisjonen, som er som følger.

Eksempler på spørsmål og diskusjon om GLBB og GLB

1. En bil beveger seg i en rett linje med en fast hastighet på 50 km / time. Hva er avstanden som kjørte med bilen etter 5 timer?

diskusjonen:

v = 50 km / time

t = 5 timer

svarte:

s = v x t

s = 50 km / t x 5 timer

s = 250 km

Så avstanden med bil etter 5 timer er 250 km.

2. Tog som beveger seg regelmessig kan kjøre en avstand på 35 m i 0,05 sekunder. Hva er hastigheten på toget?

diskusjonen:

s = 35 moh

t = 0,05 s

svarte:

v = s / t

v = 35 m / 0,05 s

v = 700 m / s

Så hastigheten på toget er 700 m / s

3. Den første forskyvningen av et objekt som beveger seg med en fast hastighet på 6 m / s er -12 m. Når nådde objektet punktet med forskyvningen på 12 m?

diskusjonen:

x = 12 moh

x₀= -12m

v = 6 m / s

svarte:

x = x₀+ v x t

12 m / s = -12 m / s + 6 t

6 t = 12 m / s + 12 m / s

t = 24 m / s: 6 s

t = 4 s

Så når objektet et punkt med en forskyvning på 12 m / s er innen 4 s.

4. Miyako er 40 m fra skoleporten. Han sykler på motorsykkel med en hastighet på 30 m / s fra skoleporten i løpet av 50 sekunder. Beregn Miyakos sluttposisjon og distansen Miyako reiste!

diskusjonen:

x₀ = 40 moh

v = 30 m / s

t = 50 s

svarte:

x = x₀ + v t

x = 40 m + (30 m / s x 50 s)

x = 40 m + 1.500 moh

x = 1.540 moh

Så avstanden Miyako reiser er s = x - x₀ = 1.540m - 40m = 1.500 m eller s = v x t = 30 m / s x 50 s = 1500 m.

5. En bil beveger seg i en rett linje med en fast hastighet på 40 m / s i 30 sekunder. Hva er distansen med bilen i løpet av denne tiden?

diskusjonen:

x₀ = 0

v = 40 m / s

t = 30 s

svarte:

x = x₀ + v t

x = 0 + (40 m / s x 30 s)

x = 1200 moh

Reist avstand kan vi finne med formelen s = x - x₀ = 1200 m - 0 = 1200 moh.

Nå fra ovenstående kan det bevise at i regelmessig rett bevegelse, avstand og forskyvning har den samme verdien.

6. En rett bevegelig bil akselereres med vanlig hastighet med en begynnelseshastighet på 35 m / s. Etter 15 sekunder blir hastigheten 50 m / s. Beregn akselerasjonen! (t₀= 0)

diskusjonen:

v₀ = 35 m / s

t₀ = 0

v = 50 m / s

t = 15 s

svarte:

7. En partikkel beveger seg med en fast akselerasjon på 4 m / s², Etter å ha beveget seg i 8 sekunder blir partikkelhastigheten 400 m / s. Bestem starthastigheten til partikkelen!

diskusjonen:

a = 4 m / s²

t = 8 s

v₀ = 400 m / s

svarte:

v = v₀+ kl

400 m / s = v₀ + (4 m / s² x 8 s)

400 m / s = v₀ + 32 m / s

v₀ = 400 m / s - 32 m / s

v₀ = 368 m / s

8. Et objekt beveger seg med en begynnelseshastighet på 2 m / s. Etter å ha beveget seg i 8 sekunder blir objektets hastighet 10 m / s. Hva er forskyvningen som gjenstanden har reist i løpet av denne tiden?

diskusjonen:

v₀ = 2 m / s

v = 10 m / s

t = 8 s

svarte:

x = (v + v₀) x 1/2 t

x = (10 m / s + 2 m / s) x (1/2 x 8 s)

x = 12 m / s x 4 s

x = 48 moh

9. En bil har en starthastighet på 3 m / s. Når forskyvningen øker med 10 m, blir hastigheten 5 m / s. Hva er akselerasjonen av bilen?

diskusjonen:

v₀ = 3 m / s