Aritmetické a geometrické vzorce s příklady otázek a jejich diskuse
Tento článek bude diskutovat o aritmetických a geometrických vzorcích spolu s příklady otázek a jejich diskusí.
Aritmetika a geometrie jsou naše témataučit se ve škole v matematice. Tam, kde při národních zkouškách, přijímacích zkouškách na vysokou školu nebo zkouškách při podání žádosti o zaměstnání často existují otázky týkající se obou.
Nejen to musíme také rozlišovatmezi aritmetickými sekvencemi a řádky nebo geometrickými sekvencemi a řádky, protože pravidla sekvencí a řádků nám mohou usnadnit provádění výpočtů, jako je bankovní úrok, zvýšení produkce a zisk / ztráta pro firmu. Dobře, podívejme se na následující vysvětlení!
Aritmetické vzorce
-
Aritmetická řada

Podívejte se na výše uvedenou tabulku a sledujte, jak se liší počty zleva doprava? A pak pozorovat rozdíl v číslech od shora dolů?
Z pozorování zjišťujeme, že rozdíl od jednoho řádku je vždy opraven. Například z našeho pravého řádku vlevo: 1, 2, 3, 4, 5 (rozdíl je 1).
5 - 1 = 4; 4 - 1 = 3; 3 - 1 = 2; 2 - 1 = 1
A shora dolů: 1, 6, 11, 16 (rozdíl 5).
16 - 5 = 11; 11 - 5 = 6; 6 - 5 = 1
Řádky jako je tento se nazývají aritmetické sekvence.
Vyvolá se rozdíl, který má pevnou hodnotu jiné a je symbolem b. Obecně lze říci, že pokud Un je slabika vzorcen aritmetická posloupnost, pak platí
b = Un - Un-1
Pokud je první funkční období (U.1) symbolizovaný a a rozdíl je symbolizován b, pak výraz vzorecn sekvence může být odvozena následovně.
U1= a
U2= U1 + b = a + b
U3= U2 + b = (a + b) + b = a + 2b
U4= U3 + b = (a + 2b) + b = a + 3b
U5= U4 + b = (a + 3b) + b = a + 4b
Podmínky tedy lze formulovatn aritmetických řad je
Un= a + (n - 1)b
Popis:
Un= tribe ton
a = první slabika
b = jiné
n = mnoho kmenů
-
Aritmetická řada
Pokud jsou aritmetické posloupnosti spojeny dohromady, získá se aritmetická posloupnost. Například U1, U2, U3, ……., Un jsou tedy kmeny aritmetických řad U1 + U2 + U3 + .... + Un volal aritmetická progrese. Aritmetická řada z n psaný s notacín s Un= a + (n - 1)b.
Obecný vzorec pro aritmetickou postupnost je
S.n= 1/2 n (a + Un)
S.n= 1/2 n (2a + (n - 1) b)
Popis:
S.n= počet aritmetických progresí
a = první slabika
b = jiné
Un= tribe ton
n = mnoho kmenů
Určete termín don aritmetická posloupnost, pokud je znát číselný vzorec n první kmen. Kmen nan lze určit podle následujícího vzorce.
Un = Sn - S.n-1
-
Řada kmenů Arisan nebo aritmetika
Pokud znáte následující aritmetickou posloupnost: U1, U2, U3, ……., Un, s mnoha aritmetickými pochodujícími kmenyje liché, takže uprostřed řádku je výraz, který rozděluje řádek na 2 stejné části. Předpokládejme, že střední termín sekvence je Ut. Takže najít střednědobý termín je následující.

Popis:
Ut= prostřední kmen aritmetických řad
a = první slabika
Un= poslední kmen aritmetických řad s mnoha n zvláštní
-
Vložit do aritmetického řádku
Například U1, U2, U3, ……., Un, je aritmetická sekvence s počáteční slabikou U1. Pokud je vloženo mezi dva po sobě jdoucí termíny k čísla tak, že se vytvoří nové aritmetické sekvence, různé nové aritmetické sekvence se vytvoří následovně.
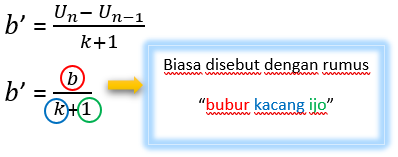
Popis:
b ’= nový rozdíl po vložení
b = jiné před vložením
k = vložené číslo
Geometrické vzorce
-
Geometrická čára
Zkuste dodržovat řádky 1, 2, 4, 8, 16, .... Podívejte se, že další člen je získán vynásobením 2 v předchozím období. Tato sekvence zahrnuje geometrickou sekvenci.
Lze tedy dospět k závěru obecně, geometrická posloupnost je posloupnost čísel, které každý kmen získaný z předchozího členu vynásobil konstantním číslem (konstantou). Tato pevná čísla jsou volána poměr (srovnání) a symbolizované r.
Pokud U1, U2, U3, U4......., Un geometrická posloupnost s Un je vzorecn, a poměr r, použitelné:
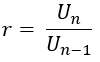
Obecný vzorec pro kmenn geometrická sekvence s prvním termínem (U1) a a poměr r, lze odvodit následovně.
U1= a
U2= U1 x r = ar
U3= U2 x r = ar²
U4= U3 x r = ar3
::
Un= Un-1 x r = arn-2 x r = arn-1
Takto byla získána geometrická posloupnost a, ar, ar², ...., arn-1.
Obecný vzorec pron geometrická sekvence je
Un= arn-1
Popis:
Un = tribe ton
a = první slabika
r = poměr
n = mnoho kmenů
-
Geometrická řada
Pokud U1, U2, U3, U4......., Un je pak řada geometrie U1 + U2 + U3+ U4 + …… .. Un je geometrická řada s Un = arn-1.
Obecný vzorec pro stanovení částek n první člen geometrické sekvence lze odvodit následovně.
Například S.n zápis částek n první slabika.
S.n = U1 + U2 + U3 + …… .. Un
S.n = a + ar + ar2 + ... .. + arn-1…………………………………………………………………(1)
Pokud jsou oba segmenty násobeny r, pak
rSn = ar + ar2 + ar3 + ... .. + arn………………………………………………………………(2)
Z rozdílu v rovnicích (1) a (2) můžeme získat

Takže vzorec součtu n první člen geometrické posloupnosti, který je následující.

Popis:
S.n = částka n první slabika
a = první slabika
r = poměr
n = mnoho kmenů
-
Centrální kmen řady Line nebo Geometry
Například znáte následující linii geometrie: U1, U2, U3, U4......., Un (počet výrazů je lichý). Středním obdobím řádku je Ut, potom je vzorec následující.
Popis:
Ut= střednědobá geometrická sekvence
a = první slabika
Un= poslední termín geometrická posloupnost s číslem n zvláštní
-
Vložit do řádku geometrie
Pokud je do geometrie vložen řádek k čísla takovým způsobem mezi dvěma po sobě jdoucími termíny, takže vznikají nové geometrické linie. Takže při hledání nového poměru lze formulovat následovně.

Popis:
r ’= nový poměr po vložení
r = poměr před vložením
k = vložené číslo

-
Neomezená geometrická řada
Nekonečná geometrická řada je geometrická řada, kterou mnoho kmenů nemůže rozřezat. Zvažte následující příklad!
a. 1 + 2 + 4 + 8 + ...
b. 5 - 10 + 20 - 40 + ...
c. 1 + 1/2 + 1/4 + 1/8 + ...
d. 9 - 3 + 1 - 1/3 + ...
Řada výše je příkladem nekonečné geometrické řady. Vezměme si příklady aab. Série je divergentní série, tj. řada, která nepřechází na určitou hodnotu a má poměr r s | r | > 1.
Dále příklady c a d jsou konvergentní série, tj. řada, která jde na určitou hodnotu a má poměr r s | r | <1.
V konvergujících řadách počet termínů nepřesáhne určitou cenu, ale přiblíží se k určité ceně. Tato konkrétní cena se nazývá nekonečný počet termínů což je označeno S∞. S hodnota∞ představuje přibližovací hodnotu (limit) celého termínu (Sn) s n blížící se nekonečno. Proto lze vzorec nekonečné řady odvodit z geometrické řady s prvním členem a, a n → ∞.

Protože se řada sbíhá (| r | <1), pro n → ∞, pak arn→ 0 tak to

Takže vzorec pro počet nekonečných geometrických řad je
Příklad otázek a diskuse
1. Určete 6. a 10. člen řádků -3, 2, 7, 12, ...
Diskuse:
a = -3
b = Un Un-1 = 2 - (-3) = 5
Un = a + (n-1) b, pak:
U6 = (-3) + (6-1) 5 = 22
U10 = (-3) + (10-1) 5 = 42
2. Najděte prvních 90 podmínek série 2 + 4 + 6 + 8 +
Diskuse:
a = 2
b = 4 - 2 = 2
n = 90
pak,
S.n= 1/2n (2a + (n-1)b)
S.n= 1/2 x 90 (2 (2) + (90-1) 2)
S.n= 45 (4 + 178)
S.n= 45 (182)
S.n= 8,190
Prvních 90 podmínek této série je 8 190.
3. Aritmetická posloupnost 3, 5, 7, 9, .... 1,007 je známa.
Určete střední období řádku.
Diskuse:
a = 3
b = 5-7 = 2
Un = 1,007, pak:
Ut = 1/2 (a + Un)
Ut = 1/2 (3 + 1 007)
Ut = 1/2 (1 010)
Ut = 505
4. Známé řádky 2, 12, 22, 32, .... Mezi dva po sobě jdoucí termíny jsou 4 čísla vložena tak, že se vytvoří nová aritmetická posloupnost. Určit:
a. Nový rozdíl
b. Vzorec pro n. Období
c. První počet n pojmů nové aritmetické posloupnosti.
Diskuse:
a.

b. Vzorec n-tého termínu je
Un = a + (n-1) b
Un = 2 + (n-1) 2
Un = 2 + (2n-2)
Un = 2n
c. Číslo prvního termínu n je
S.n= 1/2n (a + Un )
S.n= 1/2n (2 + 2n)
S.n= n (n + 1)
5. Najděte první člen, poměr a 8. člen geometrické sekvence 2, 6, 18, 54, ...
Diskuse:
a = 2
r = U2/ U1 = 6/2 = 3
pak,
Un= arn-1
U8= ar8-1
U8= 2 (38-1)
U8= 2 (37)
U8= 2 (2 187)
U8= 4,374
6. Určete počet geometrických řad 2 + 4 + 8 + 16 + ... (8 kmenů)
Diskuse:
a = 2
r = U2/ U1 = 4/2 = 2 (r> 1)
Počet řádků až do prvních 8 výrazů je smysluplný n = 8

Prvních 8 termínů geometrické řady je tedy 510.
7. Řádky geometrie jsou známé 1/8, 1/4, 1/2, 1, 2, 4, .... 2048. Určete střední období řádku.
Diskuse:
a = 1/8
r = U2/ U1 = 1/8: 1/4 = 2
Un = 2 048
pak,
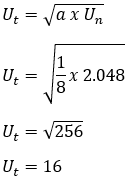
8. Je známo, že geometrická posloupnost je 1/32, 1/16, 1/8, 1/4, .... Mezi dva po sobě jdoucí termíny se vkládají tři čísla tak, že se vytvoří nová geometrická posloupnost. Určit:
a. Pozitivní poměr nových geometrických linií
b. Vzorec n-tého termínu nové geometrické sekvence
c. První počet n pojmů nového řádku geometrie.
Diskuse:
Geometrická sekvence 1/32, 1/16, 1/8, 1/4, ... nebo mohou být také doručeny 2-5, 2 -4, 2-3, 2-2, ....
a. Zvažte dva po sobě jdoucí termíny, například U1 a U2 = 1/32 a 1/16, pak:

b. Vzorec n-tého termínu je
Un= arn-1
Un= 2-5(2n / 4-1)
Un= 2n / 4-6
c. Částka n první termín je

9. Určete nekonečný počet členů geometrické řady 1 + 1/2 + 1/4 + 1/8 + ...
Diskuse:
a = 1
r = U2/ U1 = 1/2: 1 = 1/2
pak,

10. První člen geometrické řady je 2 a součet do nekonečna je 4. Najděte poměr.
Diskuse:
a = 2
S.∞ = 4
potom nahradíme vzorec S∞
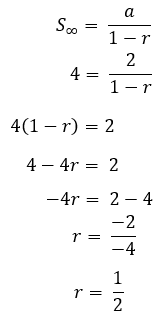
Toto je vysvětlení aritmetických a geometrických vzorců spolu s příklady otázek a jejich diskuse. Doufejme, že je to užitečné!








