質問とその考察の例を含む算術および幾何学の公式
この記事では、算術式と幾何学式、および質問の例とその説明について説明します。
算数と幾何学が私たちのトピックです数学の学校で学びます。国家試験、大学入試、または就職に向けた試験の際に、しばしば両方についての質問があります。
それだけでなく、私たちも区別する必要があります算術シーケンスと行の間、または幾何シーケンスと行の間。シーケンスと行のルールは、銀行の利息、生産の増加、ビジネスの利益/損失などの計算を完了するのに役立ちます。よし、次の説明を見てみよう!
算術式
-
算術行

上の表を見て、左から右への数値の違いを確認してください。そして、上から下への数字の違いを観察しますか?
観察から、1つのラインとの差は常に固定されていることがわかります。たとえば、右の行から左へ:1、2、3、4、5(違いは1)。
5-1 = 4; 4-1 = 3; 3-1 = 2; 2-1 = 1
そして上から下へ:1、6、11、16(違い5)。
16-5 = 11; 11-5 = 6; 6-5 = 1
このような行は、算術シーケンスと呼ばれます。
固定値を持つ差分が呼び出されます 違う と象徴されています b。 一般に、 Uん 音節の公式ですん 算術シーケンス、それが適用されます
b = Uん - Un-1
最初の用語なら (U.1) によって象徴される a そしてその違いは b、次に式ん シーケンスは次のように導出できます。
U1= a
U2= U1 + b = a + b
U3= U2 + b =(a + b)+ b = a + 2b
U4= U3 + b =(a + 2b)+ b = a + 3b
U5= U4 + b =(a + 3b)+ b = a + 4b
したがって、用語は次のように定式化できます。ん 算術ランクの
Uん= a +(n-1)b
説明:
Uん= 部族へん
a = 最初の音節
b = 違う
n = 多くの部族
-
算数シリーズ
算術シーケンスの項を合計すると、算術級数が得られます。たとえば U1、U2、U3、…………、Uん 算術ランクの部族である場合、 U1 + U2 + U3 + .... + Uん 呼ばれる 算術の進行。 からの算術級数 ん S表記で書かれたん と Uん= a +(n-1)b。
したがって、算術進行の一般的な式は
Sん= 1/2 n(a + Uん)
Sん= 1/2 n(2a +(n-1)b)
説明:
Sん= 算数の進行の数
a = 最初の音節
b = 違う
Uん= 部族へん
n = 多くの部族
用語を決定するん 数式が既知の場合の算術シーケンス ん 最初の部族。部族にん 次の式で求められます。
Uん = Sん - Sn-1
-
アリサンの中部族または算数
次の算術シーケンスがわかっている場合: U1、U2、U3、…………、Un、 多くの算術行進部族は奇数なので、線の真ん中に、線を2つの等しい部分に分割する項があります。シーケンスの中期が Ut。したがって、中期用語を見つけることは次のとおりです。

説明:
Ut= 算術ランクの中部族
a = 最初の音節
Uん= 多くの算術ランクの最後の部族 ん 奇数
-
算術行に挿入
たとえば U1、U2、U3、…………、Un、 最初の音節を持つ算術シーケンスです U1. 2つの連続する用語の間に挿入された場合 k 新しい算術シーケンスが形成されるような数、異なる新しい算術シーケンスは次のように形成されます。
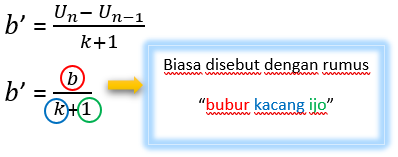
説明:
b ’= 挿入後の新しい違い
b = 挿入前は異なる
k = 挿入された番号
ジオメトリ式
-
ジオメトリライン
行1、2、4、8、16、...を観察してみてください。次の項は、前の項の2を掛けることによって得られることを確認してください。このシーケンスには、幾何学的シーケンスが含まれます。
だから、一般的に結論づけることができます、 幾何学的シーケンス 前の項から得られた各部族に定数(定数)を掛けた数のシーケンスです。これらの固定数は 比率(比較) とによって象徴 r。
もし U1、U2、U3、U4.......、Uん ジオメトリックシーケンス Uん 数式ですn、 と比率 r、 該当:
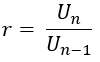
部族の一般式ん 最初の項を持つ幾何学的シーケンス(U1)宣言されている a と比率 r、 次のように導出できます。
U1= a
U2= U1 x r = ar
U3= U2 x r =ar²
U4= U3 x r = ar3
::
Uん= Un-1 x r = arn-2 x r = arn-1
このようにして得られた幾何学的シーケンス a、ar、ar²、....、arn-1.
したがって、一般的な式ん 幾何学的シーケンスは
Uん= arn-1
説明:
Uん = 部族へん
a = 最初の音節
r = 比率
n = 多くの部族
-
ジオメトリシリーズ
もし U1、U2、U3、U4.......、Uん 次に、ジオメトリの行です U1 + U2 + U3+ U4 +…….. Uん は ジオメトリシリーズ と Uん = arn-1.
金額を決定するための一般式 ん 幾何学的シーケンスの最初の項は、次のように導出できます。
たとえば Sん 金額表記 ん 最初の音節。
Sん = U1 + U2 + U3 +…….. Uん
Sん = a + ar + ar2 + ... .. + arn-1…………………………………………………………………(1)
両方のセグメントが乗算されている場合 r、 その後
rSん = ar + ar2 + ar3 + ... .. + arん………………………………………………………………(2)
式(1)と(2)の違いから、

したがって、合計式 ん 幾何学的シーケンスの最初の項。次のとおりです。

説明:
Sん = 金額 ん 最初の音節
a = 最初の音節
r = 比率
n = 多くの部族
-
ラインまたはジオメトリシリーズの中心部族
たとえば、次のジオメトリ行を知っています。 U1、U2、U3、U4.......、Uん (項の数は奇数です)。行の中期は Ut、 すると、式は次のようになります。
説明:
Ut= 中期幾何シーケンス
a = 最初の音節
Uん= 番号付きの最後の項の幾何学的シーケンス ん 奇数
-
ジオメトリ行に挿入
ジオメトリ行に挿入されている場合 k 新しい数学的線が形成されるように、2つの連続する項の間でそのような方法で番号を付けます。したがって、新しい比率を見つけるには、次のように定式化できます。

説明:
r ’= 挿入後の新しい比率
r = 挿入前の比率
k = 挿入された番号

-
無制限のジオメトリシリーズ
無限のジオメトリシリーズは、その部族の多くが切り刻むことができないジオメトリックシリーズです。次の例を考えてみましょう!
a。 1 + 2 + 4 + 8 + ...
b。 5-10 + 20-40 + ...
c。 1 + 1/2 + 1/4 + 1/8 + ...
d。 9-3 + 1-1/3 + ...
上記のシリーズは、無限のジオメトリシリーズの例です。例aとbを考えます。シリーズは 発散シリーズ、 つまり、特定の値に到達せず、比率を持つシリーズ r と| r | > 1。
次に、例cとdは 収束シリーズ、 つまり、特定の値になり、比率を持つシリーズ r と| r | <1。
収束シリーズでは、項の数は特定の価格を超えませんが、特定の価格に近づきます。この特定の価格は 無限の項 これはSで表されます∞。 S値∞ 項全体のアプローチ値(限界)を表します(Sん)と ん 無限に近づいています。したがって、無限級数公式は、最初の項を持つ幾何級数から導出できます。 a、 と n→∞。

シリーズが収束しているため(| r | <1)、 n→∞、 その後 arん→0 だから

したがって、無限の幾何学的系列の数の式は
質問とディスカッションの例
1.行-3、2、7、12、...の6番目と10番目の項を決定します。
議論:
a = -3
b = Uん Un-1 = 2-(-3)= 5
Uん = + (n-1)b、 次に:
U6 =(-3) + (6-1)5 = 22
U10 =(-3) + (10-1)5 = 42
2. 2 + 4 + 6 + 8 +シリーズの最初の90項を見つける
議論:
a = 2
b = 4-2 = 2
ん = 90
その後、
Sん= 1/2ん (2a +(n-1)b)
Sん= 1/2 x 90 (2(2)+(90-1)2)
Sん= 45(4 + 178)
Sん= 45(182)
Sん= 8,190
したがって、シリーズの最初の90項は8,190です。
3.算数列3、5、7、9、...。1,007は既知です。
ラインの中期を決定します。
議論:
a = 3
b = 5-7 = 2
Uん = 1,007、次に:
Ut = 1/2(a + Uん)
Ut = 1/2(3 + 1,007)
Ut = 1/2(1,010)
Ut = 505
4.既知の行2、12、22、32、... 2つの連続する項の間に、新しい算術シーケンスが形成されるように4つの数値が挿入されます。決定:
a。新しい違い
b。 N番目の項の式
c。新しい算術シーケンスの最初の数n項。
議論:
a。

b。 n番目の式は
Uん = + (n-1)b
Uん = 2 + (n-1)2
Uん = 2 + (2n-2)
Uん = 2n
c。最初の項nの数は
Sん= 1/2ん (a + Uん )
Sん= 1/2ん (2 + 2n)
Sん= n(n + 1)
5.ジオメトリ行2、6、18、54、...の最初の項、比率、および8番目の項を見つけます。
議論:
a = 2
r = U2/ U1 = 6/2 = 3
その後、
Uん= arn-1
U8= ar8-1
U8= 2(38-1)
U8= 2(37)
U8= 2(2,187)
U8= 4,374
6.ジオメトリシリーズの数を決定する2 + 4 + 8 + 16 + ... (8部族)
議論:
a = 2
r = U2/ U1 = 4/2 = 2(r> 1)
最初の8項までの行数は意味があります ん = 8

したがって、ジオメトリックシリーズの最初の8項は510です。
7.ジオメトリ行は、1 / 8、1 / 4、1 / 2、1、2、4、...、2048と呼ばれます。ラインの中期を決定します。
議論:
a = 1/8
r = U2/ U1 = 1/8:1/4 = 2
Uん = 2,048
その後、
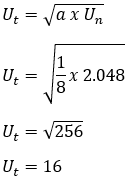
8.幾何学的シーケンスは1 / 32、1 / 16、1 / 8、1 / 4、...であることが知られています。2つの連続する項の間に、新しい幾何学的シーケンスが形成されるように3つの数値が挿入されます。決定:
a。新しい形状線の正の比率
b。新しいジオメトリシーケンスのn番目の項の式
c。新しいジオメトリ行の最初のn項。
議論:
ジオメトリシーケンス1 / 32、1 / 16、1 / 8、1 / 4、...または提供することもできます2-5, 2 -4, 2-3, 2-2、...
a。たとえば、Uのように2つの連続する用語を考えます。1 とU2 = 1/32および1/16の場合:

b。 n番目の式は
Uん= arn-1
Uん= 2-5(2n / 4-1)
Uん= 2n / 4-6
c。金額 ん 最初の用語は

9.幾何系列の項の無限数を決定する1 + 1/2 + 1/4 + 1/8 + ...
議論:
a = 1
r = U2/ U1 = 1/2:1 = 1/2
その後、

10.ジオメトリシリーズの最初の項は2であり、無限大の合計は4です。比率を見つけます。
議論:
a = 2
S∞ = 4
次に、式Sを代入します。∞
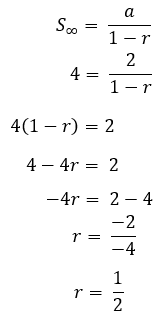
これが、算術式と幾何学式の説明と、質問の例とそれらの議論です。うまくいけば、これは便利です!








