Aritmetiske og geometriformler med eksempler på spørgsmål og deres diskussion
Denne artikel vil diskutere de aritmetiske og geometriske formler sammen med eksempler på spørgsmål og deres diskussion.
Aritmetik og geometri er vores emnerlære i skolen i matematik. Hvor der når der er nationale eksamener, universitetseksamener eller prøver til at ansøge om job, der ofte er spørgsmål om begge.
Ikke kun det, vi må også være i stand til at skelnemellem aritmetiske sekvenser og rækker eller geometriske sekvenser og rækker, fordi reglerne for sekvenser og rækker kan gøre det lettere for os at gennemføre beregninger, såsom bankrenter, produktionsstigninger og fortjeneste / tab for en virksomhed. Okay, lad os se på følgende forklaring!
Aritmetiske formler
-
Aritmetisk række

Se på tabellen ovenfor, se hvordan forskellen i tal fra venstre til højre? Og så, observer forskellen i tal fra top til bund?
Fra observationer finder vi, at forskellen fra en linje altid er fast. For eksempel fra vores højre række til venstre: 1, 2, 3, 4, 5 (forskellen er 1).
5 - 1 = 4; 4 - 1 = 3; 3 - 1 = 2; 2 - 1 = 1
Og fra top til bund: 1, 6, 11, 16 (forskel 5).
16 - 5 = 11; 11 - 5 = 6; 6 - 5 = 1
Rækker som dette kaldes aritmetiske sekvenser.
Forskel, der har en fast værdi kaldes forskel og symboliseres af b. Generelt kan det siges, at hvis Un er stavelsesformlenn en aritmetisk sekvens, så gælder den
b = Un - Un-1
Hvis den første periode (U1) symboliseret af en og forskellen symboliseres af b, derefter udtrykket formeln sekvensen kan afledes som følger.
U1= a
U2= U1 + b = a + b
U3= U2 + b = (a + b) + b = a + 2b
U4= U3 + b = (a + 2b) + b = a + 3b
U5= U4 + b = (a + 3b) + b = a + 4b
Så betingelserne kan formuleres tiln af aritmetiske rækker er
Un= a + (n - 1)b
Bemærkninger:
Un= stamme tiln
a = første stavelse
b = forskel
n = mange stammer
-
Aritmetisk serie
Hvis de aritmetiske sekvensudtryk tilføjes sammen, opnås en aritmetisk sekvens. For eksempel U1, U2, U3, ……., Un er stammer af aritmetiske rækker U1 + U2 + U3 + .... + Un kaldet aritmetisk progression. Aritmetisk serie fra n skrevet med S-notationenn med Un= a + (n - 1)b.
Så den generelle formel for aritmetisk progression er
Sn= 1/2 n (a + Un)
Sn= 1/2 n (2a + (n - 1) b)
Bemærkninger:
Sn= antal aritmetiske fremskridt
a = første stavelse
b = forskel
Un= stamme tiln
n = mange stammer
Bestem udtrykket tiln aritmetisk rækkefølge, hvis talformlen er kendt n den første stamme. Stamme tiln kan bestemmes ved følgende formel.
Un = Sn - Sn-1
-
Mellemstamme af arisansk linje eller aritmetik
Hvis du kender følgende aritmetiske rækkefølge: U1, U2, U3, ……., Un, med mange aritmetiske marcherende stammerer underligt, så der er et udtryk lige i midten af linjen, der deler linjen i 2 lige store dele. Antag, at den midterste sigt i sekvensen er Ut, Så at finde den midterste sigt er som følger.

Bemærkninger:
Ut= den midterste stamme af aritmetiske rækker
a = første stavelse
Un= sidste stamme af aritmetiske rækker med mange n ulige
-
Indsæt i aritmetisk række
For eksempel U1, U2, U3, ……., Un, er en aritmetisk sekvens med en indledende stavelse U1. Hvis der indsættes mellem to på hinanden følgende ord k tal, således at nye aritmetiske sekvenser dannes, de forskellige nye aritmetiske sekvenser dannes som følger.
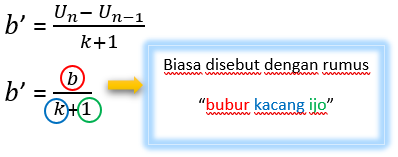
Bemærkninger:
b '= ny forskel efter indsættelser
b = forskellig inden indsættelser
k = indsat nummer
Geometri-formler
-
Geometri Line
Forsøg at observere rækkerne 1, 2, 4, 8, 16, .... Se, at det næste udtryk opnås ved at multiplicere 2 i det forrige sigt. Denne sekvens inkluderer den geometriske sekvens.
Så det kan konkluderes generelt, geometrisk rækkefølge er en sekvens af tal hver stamme opnået fra det foregående udtryk ganget med et konstant tal (konstant). Disse faste numre kaldes forhold (sammenligning) og symboliseret af r.
hvis U1, U2, U3, U4......., Un geometrisk sekvens med Un er formlen tiln, og forhold r, anvendelse:
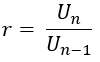
Generel formel for stammenn geometrisk sekvens med første termin (U1) er erklæret en og forhold r, kan afledes som følger.
U1= a
U2= U1 x r = ar
U3= U2 x r = ar²
U4= U3 x r = ar3
::
Un= Un-1 x r = arn-2 x r = arn-1
Dermed opnået geometrisk sekvens a, ar, ar², ...., arn-1.
Så den generelle formel forn geometrisk sekvens er
Un= arn-1
Bemærkninger:
Un = stamme tiln
a = første stavelse
r = forholdet
n = mange stammer
-
Geometry Series
hvis U1, U2, U3, U4......., Un er en række geometri derefter U1 + U2 + U3 + U4 + …… .. Un er en geometri-serie med Un = arn-1.
Generel formel til bestemmelse af beløb n den første term i den geometriske sekvens kan afledes som følger.
For eksempel Sn notering af beløb n første stavelse.
Sn = U1 + U2 + U3 + …… .. Un
Sn = en + ar + ar2 + ... .. + arn-1...........................................................................(1)
Hvis begge segmenter ganges r, derefter
rSn = ar + ar2 + ar3 + ... .. + arn........................................................................(2)
Fra forskellen i ligninger (1) og (2) kan vi få

Så summen formel n den første term i den geometriske sekvens, som er som følger.

Bemærkninger:
Sn = beløbet n første stavelse
a = første stavelse
r = forholdet
n = mange stammer
-
Central Tribe of the Line eller Geometry Series
For eksempel kender du følgende geometri linje: U1, U2, U3, U4......., Un (antallet af udtryk er ulige). Linjens midterste sigt er Ut, så er formlen som følger.
Bemærkninger:
Ut= midtvejs geometrisk sekvens
a = første stavelse
Un= den sidste term geometriske sekvens med nummer n ulige
-
Indsæt i geometri række
Hvis der er placeret geometri række k numre på en sådan måde mellem to på hinanden følgende termer, så der dannes nye geometriske linjer. Så ved at finde det nye forhold kan formuleres som følger.

Bemærkninger:
r '= nyt forhold efter indsættelse
r = forhold inden indsættelse
k = indsat nummer

-
Ubegrænset geometri-serie
En uendelig geometri-serie er en geometrisk serie, der ikke kan hugges af mange af dens stammer. Overvej følgende eksempel!
a. 1 + 2 + 4 + 8 + ...
b. 5 - 10 + 20 - 40 + ...
c. 1 + 1/2 + 1/4 + 1/8 + ...
d. 9 - 3 + 1 - 1/3 + ...
Serien ovenfor er et eksempel på en uendelig geometri-serie. Overvej eksemplerne a og b. Serien er divergerende serie, dvs. en serie, der ikke går til en bestemt værdi og har et forhold r med | r | > 1.
Dernæst er eksempler c og d konvergent serie, dvs. en serie, der går til en bestemt værdi og har et forhold r med | r | <1.
I konvergerende serier vil antallet af vilkår ikke overstige en bestemt pris, men nærmer sig en bestemt pris. Denne særlige pris kaldes uendeligt antal udtryk som er betegnet med S∞. S-værdi∞ repræsenterer tilgangsværdien (grænsen) for hele termen (Sn) med n nærmer sig uendelig. Derfor kan den uendelige serieformel afledes fra den geometriske serie med det første udtryk a, og n → ∞.

Fordi serien konvergerer (| r | <1), for n → ∞, derefter arn→ 0 så det

Så formlen for antallet af uendelige geometriske serier er
Eksempel Spørgsmål og diskussion
1. Bestem det 6. og 10. udtryk for rækkerne -3, 2, 7, 12, ...
diskussion:
en = -3
b = Un - Un-1 = 2 - (-3) = 5
Un = a + (n-1) b, derefter:
U6 = (-3) + (6-1) 5 = 22
U10 = (-3) + (10-1) 5 = 42
2. Find de første 90 udtryk i serien 2 + 4 + 6 + 8 +
diskussion:
en = 2
b = 4 - 2 = 2
n = 90
derefter,
Sn= 1/2n (2en + (n-1)b)
Sn= 1/2 x 90 (2 (2) + (90-1) 2)
Sn= 45 (4 + 178)
Sn= 45 (182)
Sn= 8.190
Så de første 90 udtryk i serien er 8.190.
3. Aritmetisk sekvens 3, 5, 7, 9, .... 1.007 er kendt.
Bestem linjens midterste sigt.
diskussion:
a = 3
b = 5-7 = 2
Un = 1.007, derefter:
Ut = 1/2 (en + Un)
Ut = 1/2 (3 + 1.007)
Ut = 1/2 (1.010)
Ut = 505
4. Kendte rækker 2, 12, 22, 32, .... Mellem to på hinanden følgende ord indsættes 4 numre på en sådan måde, at der dannes en ny aritmetisk sekvens. Angiv:
a. En ny forskel
b. Niende formel
c. Det første tal n udtryk i den nye aritmetiske sekvens.
diskussion:
a.

b. Den niende formel er
Un = a + (n-1) b
Un = 2 + (n-1) 2
Un = 2 + (2n-2)
Un = 2n
c. Nummeret for den første periode n er
Sn= 1/2n (en + Un )
Sn= 1/2n (2 + 2n)
Sn= n (n + 1)
5. Find den første term, forholdet og den 8. term i den geometriske sekvens 2, 6, 18, 54, ...
diskussion:
a = 2
r = U2/ U1 = 6/2 = 3
derefter,
Un= arn-1
U8= ar8-1
U8= 2 (38-1)
U8= 2 (37)
U8= 2 (2.187)
U8= 4,374
6. Bestem antallet af geometri-serier 2 + 4 + 8 + 16 + ... (8 stammer)
diskussion:
en = 2
r = U2/ U1 = 4/2 = 2 (r> 1)
Antallet af rækker op til de første 8 termer er meningsfuldt n = 8

Så de første 8 udtryk i den geometriske serie er 510.
7. Geometri-rækker er kendt 1/8, 1/4, 1/2, 1, 2, 4, .... 2048. Bestem linjens midterste sigt.
diskussion:
a = 1/8
r = U2/ U1 = 1/8: 1/4 = 2
Un = 2.048
derefter,
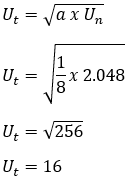
8. Det vides, at den geometriske sekvens er 1/32, 1/16, 1/8, 1/4, .... Mellem to på hinanden følgende ord indsættes tre tal på en sådan måde, at der dannes en ny geometrisk sekvens. Angiv:
a. Positivt forhold mellem nye geometrislinjer
b. Den niende terminformel i den nye geometriesekvens
c. Det første tal n udtryk i den nye geometri række.
diskussion:
Geometriesekvens 1/32, 1/16, 1/8, 1/4, ... eller kan også serveres 2-5, 2 -4, 2-3, 2-2, ....
a. Overvej to på hinanden følgende termer, for eksempel U1 og U2 = 1/32 og 1/16, derefter:

b. Den niende formel er
Un= arn-1
Un= 2-5(2n / 4-1)
Un= 2n / 4-6
c. Beløbet n første valgperiode er

9. Bestem det uendelige antal udtryk i den geometriske serie 1 + 1/2 + 1/4 + 1/8 + ...
diskussion:
a = 1
r = U2/ U1 = 1/2: 1 = 1/2
derefter,

10. Den første term i en geometri-serie er 2, og summen til uendelig er 4. Find forholdet.
diskussion:
a = 2
S∞ = 4
derefter erstatter vi formlen S∞
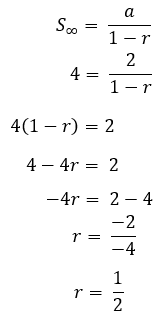
Det er forklaringen på aritmetiske og geometriformler sammen med eksempler på spørgsmål og deres diskussion. Forhåbentlig er dette nyttigt!








