Zbirka formula trigonometrije s primjerima pitanja i njihova rasprava

Za one od vas koji ste još studenta oni koji su radili moraju studirati matematiku. Taj se predmet doista učio studentima od osnovne škole pa sve do studenata na sveučilištu.

Čak je i matematika uvijek uključena u školske ispite i državne ispite na nekoliko razina obrazovanja.

Jer je i ovaj predmet prepun učenikakoji se često žali kad dobije zadatak da radi matematičke probleme. Zaista su neke formule u matematici dovoljne da bi se napustio razum koji bi mogao biti shvaćen. Jedna matematička formula koju je prilično teško naučiti je trigonometrijska formula.

Sadržaj

Zbirka formula trigonometrije

Razgovarajte o formulama trigonometrije pa vinaučit će o oblicima trokuta. Jer trigonometrijska formula je formula koja proučava odnos kutova i strana koje postoje u obliku trokuta. Dok je sama trigonometrijska funkcija podijeljena na tri, i to na funkciju consinus (cos), sine (sin), secan (sec), tangenta (tan), cotangen (cotan) i sesecan (cosec).

1. Formula funkcije trigonometrije

Prva trigonometrijska formula dolazi iz gornjih trigonometrijskih funkcija. Gdje svaka formula ima način izračuna iz svakog ugla trokuta. Formula trigonometrijske funkcije je

Za formulu se za izračunavanje stranica koristi αprednja strana podijeljena nagnutom stranom. Dok se formula cos α koristi za izračun strane podijeljene s hipotenuzom. A tan α je formula s prednje strane hipotenuze u trokutu. Da biste lakše upamtili gore navedene tri formule, možete upotrijebiti sljedeće kratice.

SinDeMi

Skraćenica kosog prednjeg sinusa ili sin α formula.

CosSaMi

Lean kozmetika ili cos α formula.

TanDeSa

A kratica TanDeSa znači Side Front Tangent ili tan α formula.

2. Formule identiteta trigonometrije

Trigonometrijska formula identiteta je formulausporedite trigonometriju s x varijablama kuta. Gdje je varijabla x dobijena iz mjere stupnjeva i radijana. Dok je način da se riješi jednadžba sin xº = sin? ° (x? R) je:

Prvo upotrijebite omjer kuta sin (180º -? º) = sin? º i sin (? º + k.360º) = sin? º. Zatim uđite u jednadžbu sin xº = sin? º biti

Ako je grijeh x⁰ = grijeh?⁰ (x? R), zatim:

x =? + k.360⁰ ili x = (180)⁰ ? ?) + k.360, s k? B

Napomena: x je u stupnjevima

Ako je sin x = sin A (x? R), tada:

x = A + k.2? ili x = (? A) + k.2?, sa k? B

Napomena: x je u radijanima

3. Količina i razlika trigonometrije kuta

Treća formula u trigonometriji je formula za zbroj i razlike u trigonometrijskim kutovima. Formula je:

Ova se formula koristi za zbrajanje kutova i strana trokuta.

4. Formula množenja trigonometrije

Što se tiče množenja u kutovima i stranama trokuta, možete upotrijebiti gornju formulu za množenje trigonometrijskog oblika.

5. Formule količine i razlike trigonometrije

U trokutu ne postoji samo formula dodavanja, već postoji i strana koja se mora zbrojiti istodobno tražeći razliku s gornjom formulom za zbroj i trigonometrijsku razliku.

6. Trigonometrija dvostruke i tri kutne formule

trigonometrijska dvokutna-trostruka formula

Ako pronađete problem u kutovima 2 i 3 trokuta, tada upotrijebite formulu 2 i 3 u trigonometriji.

7. Formula polumjera trigonometrije

trigonometrijska formula u obliku polukruga

Kutovi koji se mogu izračunati na trokutu nisu samo puni kutovi, već i pola kuta trokuta, mogu se izračunati gornjom formulom trigonometrijskih polukutova.

8. Formule za specijalne kutove trigonometrije

Pored sedam gornjih formula, u formuli trigonometrije postoje i posebni uglovi

$0 ^ {o}$ , $30 ^ {o}$ , $45 ^ {o}$ , $60 ^ {o}$ , i $90 ^ {o}$ , Gdje za svaku posebnu kutnu formuluTrigonometriju možete vidjeti na gornjem grafikonu. Što se tiče formule za pronalaženje trigonometrijskih vrijednosti koje imaju neke veze sa posebnim kutom iznad, upotrijebite sljedeću formulu.

Pa kad radite na problemutrigonometrija tada morate unaprijed otkriti je li problem problem s uobičajenom formulom trigonometrije ili s posebnom formulom trigonometrijskog problema. Jer svaka formula koju koristite dat će različite rezultate kao i točnost u odgovaranju na pitanja.

Primjeri trigonometrije

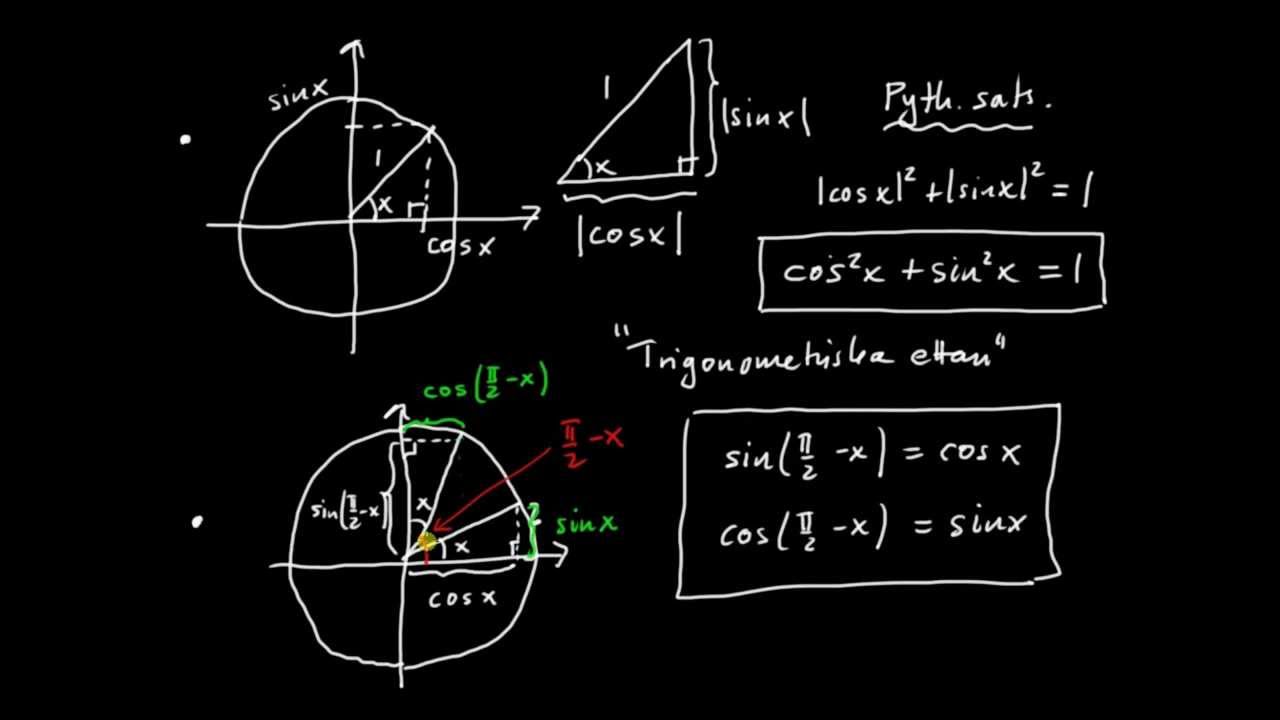
Formule trigonometrije i problemi sa uzorcima

Kako to učiniti? Razumijete li o gornjoj trigonometrijskoj formuli? Zapravo, formula je prilično teška za razumjeti, ali to ne znači da ne možete ako nastavite pokušavati. Trigonometrijske formule možete razumjeti i kroz trigonometrijske probleme. Što se tiče nekih primjera pitanja o trigonometriji koje možete isprobati su:

1. Odredite vrijednost sin 105º + sin 15º

Gore navedeni trigonometrijski problem problem je trigonometrije vrste dodavanja, tako da možete koristiti adicijsku trigonometrijsku formulu koja je 2 sin ½ (A + B) cos ½ (A-B). Postupak je:

vrijednost sin 105 ° + sin 15 ° = 2 sin ½ (105 + 15) ° cos ½ (105-15) °
= 2 sin ½ (102) ° cos ½ (90) °
= sin 60 ° cos 45 °

Dakle, odgovor na problem grijeh 105º + sin 15º je grijeh 60º cos 45º.

2. Pronađite vrijednost jednadžbe sin xº sin 25º

Rješavanje gornjih pitanja, naime:

x = 25⁰ + k.360⁰ ili x = (180)⁰ ? 25⁰) + k.360⁰

= 155⁰ + k.360⁰

Dakle, x = 25⁰ + k.360⁰ ili 155º + k.360⁰

Dakle, vrijednost jednadžbe sin xº sin 25º je x = 25⁰ + k.360⁰ ili 155º + k.360^0.

3. Odredite vrijednost množenja 2 cos 75º cos 15º

Treći problem je iznad modela trigonometrijskog množenja. Upotrijebljena formula je 2 cos A cos B = cos (A + B) + cos (A-B). Rješenje problema je:

2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75 - 15) °
= cos 90 ° + cos 60 °
= 0 + ½
= ½

Dakle, rezultat množenja 2 cos 75º cos 15º je ½.

4. a trokut ABC oštra točka, poznata cos A = 4/5 i sin B = 12/13, onda je sin C jednak ...

Budući da trokut ABC ima oštar kut, tada su i kutovi A, B i C akutni, pa:

cos A = 4/5, tada je sin A = 3/5,
sin B = 12/13, onda je cos B = 5/13
A + B + C = 180 °, (broj kutova u jednom trokutu = 180)
A + B = 180 - C
grijeh (A + B) = grijeh (180 - C)
grijeh A. cos B + cos A.sin B = sin C, (kutovi međusobno povezanih trokuta: sin (180-x) = sin x)
sin C = sin A.cos B + cos A.sin B
sin C = 3 / 5,5 / 13 + 4 / 5,12 / 13
sin C = 15/65 + 48/65 = 63/65

Iz gornje formule vrijednost sin C je 63/65

5. Odlučite vrijednost grijeha 120^o

Za pitanje broj 5 postoje dva načina da se to riješi. Prvi način je:

120 = 90 + 30

Dakle, grijeh 120^o može se izračunati formulom Sin 120^o = Grijeh (90^o + 30^o) = Cos 30^o (dobivena je pozitivna vrijednost jer se 120 ° nalazi u kvadrantu II (2), pa je rezultat također pozitivan)
Cos 30^o = ½ √3

Ili na drugi način, naime:

Isto kao 180^o-80^º

Grijeh 120^o = Grijeh (180)^o - 60^o) = grijeh 60^o = ½ √3

Dakle, rezultat grijeha 120º je ½ √3.

6. a Trokut ABC ima bočnu dužinu AB = 6 cm, BC = 8 cm AC = 7 cm. Vrijednost cos A je ..

Kako napraviti gornji problem je s formulom:

Cos A = (AB² + AC²-BC²) / 2 (AB. AC)
Cos A = 6² + 7²-8² / 2 (6. 7)
Cos A = 36 + 49-64 / 2 (42)
Cos A = 21/84

Tako da se nalazi cos A 21/84.

7. Točke P i Q izražene su polarnim koordinatama. Zatim odredite udaljenost između točaka P i Q!

Za gornji problem koristite formulu consinus koja glasi:

Jačina kuta POQ = 180^o - (75.)^o45^o) = 60^o.
PQ² = OQ² + OP² - 2.OQ.OP cos ∠POQ
PQ² = 3² + 5² - 2.3.5 cos 60^o c
PQ² = 9 + 25 - 30. 0,5
PQ² = 9 + 25 -15
PQ² = 19
PQ = √19 = 4,36